Als \(\mathbf{A}\) een lineaire transformatie is en \(\bar v\) een element uit een vectorruimte \(V\) dan is er iets speciaals met de vergelijking:

\(\mathbf{A} \bar v = \lambda \bar v\) , waarin \(\lambda\) een getal is.

Deze vergelijking heeft altijd de oplossing \(\bar v = \bar 0\). Ofwel de oorsprong \(\bar 0\) wordt altijd weer op de oorsprong afgebeeld.

Wat als we de vergelijking niet in \(\bar v\) willen oplossen maar in \(\lambda\) voor \(\bar v \ne \bar 0\)? Het blijkt dat voor een willekeurig gekozen \(\bar v\) dit niet mogelijk is. Maar er zijn wel combinaties van \(\lambda\) en \(\bar v\) te vinden die aan de vergelijking voldoen. De meetkundige interpretatie bij het oplossen van een dergelijke vergelijking is dat we op zoek zijn naar deelruimten \(V_d\) (lijnen,vlakken,...) van \(V\) die zelf ook weer een vectorruimte zijn en die door de transformatie \(\mathbf{A}\) onveranderd blijven. De deelruimten gaan dus altijd door de oorsprong. Bijvoorbeeld ligt \(\bar v\) op een lijn door de oorsprong en geldt het zelfde voor het beeld \(\mathbf{A} \bar v\) dan zal iedere andere \(\bar u\) op die lijn ook weer op die lijn worden afgebeeld. Daarnaast zal ieder beeld op die lijn een "vergroting" met factor \(\lambda\) van zijn origineel zijn.

Een voorbeeld in twee dimensies: Gegeven is de transformatie

\(\mathbf{A}=\left( \begin{array}{cc} 1 & 0 \\ 0 & -2 \end{array}\right)\)

Deze transformatie is een spiegeling in de \(x\)-as waarbij het spiegelbeeld twee keer vergroot wordt. De combinatie \(\lambda_1=1\) samen met vectoren van de vorm \(\bar v_1=\left(\begin{array}{c} x \\ 0 \end{array}\right)\) (=\(x\)-as) voldoen aan de vergelijking evenals de combinatie \(\lambda_2=-2\) en vectoren van de vorm \(\bar v_2=\left(\begin{array}{c} 0 \\ y \end{array}\right)\) (=\(y\)-as). De \(x\)-as en de \(y\)-as worden dus op zichzelf afgebeeld.

Overtuig jezelf door de vector \(\bar v\) te veranderen. Zijn er ook nog andere lijnen die door de oorsprong gaan en waarvan het beeld van een vector op die lijn weer op die lijn ligt?

Onderzoek met de applet welke twee lijnen onveranderlijk zijn en hoe groot de schalingsfactoren voor die lijnen zijn voor de transformatie

\(\mathbf{A}=\left( \begin{array}{cc} -3 & 0 \\ 0 & 2 \end{array}\right)\)

De waarden \(\lambda_1=1\) en \(\lambda_2=-2\) noemt men de eigenwaarden (karakteristieke waarde) van de matrix ofwel lineaire transformatie. In de deelruimte die op zichzelf wordt afgebeeld noemt men een willekeurige vector een \(eigenvector\). De eigenvectoren die bij verschillende eigenwaarden horen zijn lineair onafhankelijk. Dat wil zeggen dat ze niet in de zelfde onveranderlijke deelruimte liggen. Als bijvoorbeeld twee deelruimten lijnen zijn dan betekent dit dat er geen constante \(c\) te vinden is zodanig dat \(\bar v_1=c\bar v_2\), ofwel de lijnen vallen niet samen, maar snijden in \(\bar{0}\).

Als in een twee (of n) dimensionale ruimte twee (of n) vectoren onderling onafhankelijk zijn dan kan iedere andere vector in die ruimte worden geschreven als een unieke lineaire combinatie van die twee( of n) vectoren, ofwel
\(\bar u=c_1\bar v_1+c_2\bar v_2 \;\;;\;\; \bar u=c_1\bar v_1+c_2\bar v_2+ \ldots +c_n\bar v_n \)
Voor het beeld van \(\bar u\) geldt dan

\(\mathbf{A}\bar u=\mathbf{A}(c_1\bar v_1+c_2\bar v_2)=c_1\mathbf{A}\bar v_1+c_2\mathbf{A}\bar v_2=c_1\lambda_1\bar v_1+c_2\lambda_2\bar v_2\)

Ofwel het beeld van \(\bar u\) gaat met de zelfde coëfficienten \(c_1\) en \(c_2\) over in een lineaire combinatie van de beelden van de eigenvectoren.

Eigenwaarde en de karakteristieke vergelijking

Beschouw weer de vergelijking

\(\mathbf{A} \bar v = \lambda \bar v\) , waarin \(\lambda\) een getal is.

Deze kan worden herschreven tot

\(\mathbf{A} \bar v - \lambda \bar v = \left(\mathbf{A} - \lambda\mathbf{I}\right)\bar v =\bar{0}\), hierin is \(\mathbf{I}\) de eenheidsmatrix (enen op de diagonaal van linksboven naar rechtsonder en verder 0).

Omdat we op zoek zijn naar oplossingen waarvoor \(\bar v\ne \bar 0\) moeten we opzoek naar combinaties \(\lambda\) en \(\bar v\) waarvoor dit gaat gelden. Zonder bewijs geven we hier de methode om tot een karakteristieke vergelijking te komen waaruit \(\lambda\) kan worden berekend. Daarvoor moeten we eerst de determinant van een vierkante matrix introduceren. We geven eerst een rekenrecept voor twee dimensies. Daarna geven we het recept voor drie dimensies.

Gegeven is de vierkante \(2\times2\) matrix

\(\mathbf{A}=\left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right)\)

De determinant \(\det(\mathbf{A})\) van een 2×2 matrix \(\mathbf{A}\) is een getal verkregen door het volgende recept

\(\det(\mathbf{A})= \left| \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right| = a_{11}\cdota_{22}-a_{12}\cdota_{21}\).

Voorbeeld: Bepaal de determinant van de matrix \(\mathbf{A}=\left( \begin{array}{cc} 2 & 1 \\ 4 & 3 \end{array}\right)\).
\(\det(\mathbf{A})=2\cdot3-4\cdot1=2\)

Gegeven is de vierkante \(3\times3\) matrix

\(\mathbf{A}=\left( \begin{array}{cc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right)\)

De determinant \(\det(\mathbf{A})\) van \(\mathbf{A}\) matrix kan volgens de methode van Sarrus worden uitgerekend. Plak daartoe twee kopiën van de matrix achter elkaar. Vermenigvuldig de getallen die in drietallen langs de lijnen staan met elkaar. De getallen die je dan langs de doorgetrokken lijnen krijgt tel je bij elkaar op. Dat doe je ook voor de gestippelde lijnen. Vervolgens trek je het totaal van de gestippelde lijnen af van het totaal van doorgetrokken lijnen. Ofwel

\( \begin{array}{ll} \det(\mathbf{A}) & = \left| \begin{array}{cc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right| \\ & =a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33} \end{array}\)

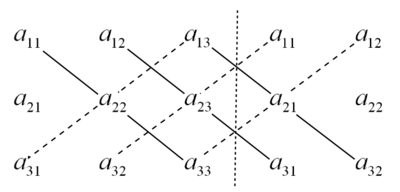
Voorbeeld: Bepaal de determinant van de matrix \(\mathbf{B}=\left( \begin{array}{cc} 1 & 2 & 3 \\ 0 & 0 & 1 \\ 1 & 0 & 1\end{array}\right)\)
\(\det(\mathbf{B})=1\cdot0\cdot1+2\cdot1\cdot1+3\cdot0\cdot0-3\cdot0\cdot1-1\cdot1\cdot0-2\cdot0\cdot1=2\)

Voor het berekenen voor de determinant van vierkante matrices in hogere dimensie verwijzen we je naar wikipedia. Daar vind je ook nog andere eigenschappen van determinanten die we voor deze cursus niet nodig hebben.

Nu terug naar het vinden van de eigenwaarden en eigenvectoren uit de vergelijking

\(\left(\mathbf{A} - \lambda \mathbf{I}\right)\bar v =\bar{0}\).

Ook hier beginnen we weer in twee dimensies. Laat

\(\mathbf{A}=\left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right)\)

Dan is

\(\left(\mathbf{A} - \lambda \mathbf{I}\right)\bar v =\bar{0}\).

te schrijven als

\(\left(\left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right) - \lambda \left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right)\right)\bar v = \left( \begin{array}{cc} a_{11}-\lambda & a_{12} \\ a_{21} & a_{22}-\lambda \end{array}\right)\bar v=0\)

Het blijkt nu te gelden dat we \(\lambda\) kunnen bepalen door de determinant van \(\left(\mathbf{A} - \lambda \mathbf{I}\right)\) gelijk te stellen aan 0. Een determinant 0 betekent dat de rijen ( en ook de kolommen ) in de matrix lineair afhankelijk zijn. Dit leidt tot de karakteristieke vergelijking:

\(\left|\mathbf{A} - \lambda \mathbf{I}\right|=\left| \begin{array}{ll} a_{11}-\lambda & a_{12} \\ a_{21} & a_{22}-\lambda \end{array}\right|=(a_{11}-\lambda)(a_{22}-\lambda)-a_{12}a_{21}=0\)

Dit is een kwadratische vergelijking in \(\lambda\). Een kwadratische vergelijking heeft niet altijd een oplossing als \(\lambda\) een reëel getal zou moeten zijn. Die beperking hoeven we ons echter niet op te leggen. Sterker nog die beperking is zelfs ongewenst. In de complexe ruimte (zie de sectie complexe getallen) heeft een kwadratische vergelijking altijd twee (mogelijk samenvallende) oplossingen \(\lambda_1\) en \(\lambda_2\). Hebben we twee eigenwaarden gevonden dan kunnen de bijbehorende eigenvectoren worden verkregen door \(\bar v_1\) en \(\bar v_2\) op te lossen uit: \(\left(\mathbf{A} - \lambda_1\mathbf{I} \right)\bar v_1=\bar 0 \) en \(\left(\mathbf{A} -\lambda_2\mathbf{I} \right)\bar v_2=\bar 0 \).

Voorbeeld:
Bepaal de eigenwaarden en de eigenvectoren van de matrix \(\mathbf{A}=\left( \begin{array}{cc} 4 & -2 \\ 3 & -1 \end{array}\right)\).
\(\det(\mathbf{A}-\lambda\mathbf{I})=\left| \begin{array}{ll} 4-\lambda & -2 \\ 3 & -1-\lambda \end{array}\right|=\)
\((4-\lambda)(-1-\lambda)+6=\lambda^2-3\lambda+2=\)
\((\lambda-1)(\lambda-2)=0\)

Hier uit volgt dat \(\lambda_1=1\) en \(\lambda_2=2\) de gevraagde eigenwaarden zijn.

\(\lambda_1=1\): Los nu op \(\left(\mathbf{A}-1\mathbf{I}\right) \bar{v}_{1} = \bar{0} \)

\(\left( \begin{array}{cc} 3 & -2 \\ 3 & -2 \end{array} \right) \left( \begin{array}{c} v_{1x} \\ v_{1y} \end{array}\right) = \left( \begin{array}{c} 0 \\ 0 \end{array}\right) \Leftrightarrow \left\{\begin{array}{c} 3v_{1x}-2v_{1y}=0 \\ 3v_{1x}-2v_{1y}=0\end{array}\right.\)
Beide vergelijkingen geven \(3v_{1x}=2v_{1y}\) ofwel \(3v_{1x}/2=v_{1y}\). We kunnen nu een willekeurige \(x\) coördinaat kiezen b.v \(v_{1x}=2 \Rightarrow v_{1y}=3\). Een eigenvector is dan
\(\bar v_1 = \left( \begin{array}{c} 2 \\ 3 \end{array}\right)\)

\(\lambda_2=2\): Los nu op \(\left(\mathbf{A}-2\mathbf{I}\right) \bar v_2 = \bar 0 \)
\(\left( \begin{array}{cc} 2 & -2 \\ 3 & -3 \end{array}\right)\left( \begin{array}{c} v_{2x} \\ v_{2y}\end{array}\right)= \left( \begin{array}{c} 0 \\ 0 \end{array}\right) \Leftrightarrow \left\{\begin{array}{c} 2v_{2x}-2v_{2y}=0 \\ 3v_{1x}-3v_{2y}=0\end{array}\right.\)
Beide vergelijkingen geven \(v_{2x}=v_{2y}\). We kunnen nu een willekeurige \(x\) coördinaat kiezen b.v \(v_{2x}=1 \Rightarrow v_{2y}=1\). Een eigenvector is dan
\(\bar v_2 = \left( \begin{array}{c} 1 \\ 1 \end{array}\right)\)

Vectoren op de lijn \(y=x\) worden dus met een factor 2 verlengd en vectoren op de lijn \(y=3x/2\) worden precies op de zelfde plek afgebeeld.

Controleer dit in de bovenstaande applet.

Laat met een berekening zien dat het beeld van \(\bar u = 2\cdot\bar v_1 - 2\cdot\bar v_2 = \left( \begin{array}{c} 2 \\ 4 \end{array}\right) \) gelijk is aan \(\bar u' = 2\cdot1\cdot\bar v_1 - 2\cdot2\cdot\bar v_2 = \left( \begin{array}{c} 0 \\ 2 \end{array}\right) = \mathbf{A}\bar u\).

In bovenstaand voorbeeld waren de eigenwaarden reële getallen. Het kan ook zijn dat er twee complexe eigenwaarden zijn. De eigenvectoren zijn dan ook complex. Complexe eigenwaarden horen bij matrices waarin een rotatie aanwezig is. We bekijken weer een voorbeeld.

Bepaal de eigenwaarden en eigenvectoren voor de matrix \(\mathbf{A}=\left( \begin{array}{cc} 1 & -1 \\ 2 & 3 \end{array}\right)\).
\(\det(\mathbf{A}-\lambda\mathbf{I})=\left| \begin{array}{ll} 1-\lambda & -1 \\ 2 & 3-\lambda \end{array}\right|=\)
\((1-\lambda)(3-\lambda)+2 =\lambda^2-4\lambda+3+2=\)
\((\lambda-2)^2+1=0\)
Hier uit volgt dat \(\lambda_1=2+i\) en \(\lambda_2=2-i\) de gevraagde eigenwaarden zijn.
\(\lambda_1=2+i\): Los nu op \(\left(\mathbf{A}-(2+i)\mathbf{I}\right) \bar v_1 = \bar 0 \)
\(\left( \begin{array}{cc} -1-i & -1 \\ 2 & 1-i \end{array}\right)\left( \begin{array}{c} v_{1x} \\ v_{1y} \end{array}\right)=\left( \begin{array}{c} 0 \\ 0 \end{array}\right)\Leftrightarrow \left\{\begin{array}{c}-(1+i)v_{1x}-v_{1y}=0 \\ 2v_{1x}+(1-i)iv_{1y}=0\end{array}\right.\)
Beide vergelijkingen geven \((-1-i)v_{1x}=v_{1y}\). We kunnen nu weer een willekeurige \(y\) coördinaat kiezen b.v \(v_{1y}=1 \Rightarrow v_{1x}=-1-i\). Een eigenvector is dan
\(\bar v_1 = \left( \begin{array}{c} -1-i \\ 1 \end{array}\right)\)

\(\lambda_2=2-i\): Los nu op \(\left(\mathbf{A}-(2-i)\mathbf{I}\right) \bar v_2 = \bar 0 \)
\(\left( \begin{array}{cc} -1+i & -1 \\ 2 & 1+i \end{array}\right)\left(\begin{array}{c} v_{2x} \\ v_{2y}\end{array}\right)=\left( \begin{array}{c} 0 \\ 0 \end{array}\right) \Leftrightarrow \left\{\begin{array}{c}(-1+i)v_{2x}-v_{2y}=0 \\ 2v_{1x}+(i+1)v_{2y}=0\end{array}\right.\)
Beide vergelijkingen geven \((-1+i)v_{2x}=v_{2y}\). We kunnen nu een willekeurige \(y\) coördinaat kiezen b.v \(v_{2y}=1 \Rightarrow v_{2x}=-1+i\). Een eigenvector is dan
\(\bar v_2 = \left( \begin{array}{c} -1+i \\ 1 \end{array}\right)\)

Als laatste is er nog het geval van twee samenvallende eigenwaarden ofwel één reële eigenwaarde met multipliciteit twee. Het vinden van twee verschillende onafhankelijke eigenvectoren behoeft dan wat extra uitleg. Bij één reële eigenwaarde kunnen we direct één eigevector \(\bar v_1\) bepalen. Voor deze eigenvector geldt natuurlijk \((\mathbf{A}-\lambda\mathbf{I})\bar v=\bar 0\). Het blijkt nu dat voor een eigenwaarde met multipliciteit twee soms een tweede eigenvector gevonden kan worden door de vergelijking \((\mathbf{A}-\lambda\mathbf{I})^2\bar v_2=\bar 0\) op te lossen. Is dit niet het geval dan kiezen we een wilekeurige onafhankelijke vector om de ruimte op te spannen. \((\mathbf{A}-\lambda\mathbf{I})^2\bar v_2=\bar 0\) is ook te schrijven is als \((\mathbf{A}-\lambda\mathbf{I})\left((\mathbf{A}-\lambda\mathbf{I})\bar v_2\right)=\bar 0\) ligt \(\bar v_2\) of in de zelfde deelruimte als \(\bar v_1\), maar dan zijn de twee eigenvectoren niet onafhankelijk, of \(\bar v_2\) ligt in de deelruimte die door de matrix \((\mathbf{A}-\lambda\mathbf{I})\) wordt afgebeeld op de deelruimte die door \(\bar v_1\) wordt opgespannen.

Bepaal de eigenwaarden en eigenvectoren voor de matrix \(\mathbf{A}=\left( \begin{array}{cc} 1 & -1 \\ 1 & 3 \end{array}\right)\).
\(\det(\mathbf{A}-\lambda\mathbf{I})=\left| \begin{array}{ll} 1-\lambda & -1 \\ 1 & 3-\lambda \end{array}\right|=(1-\lambda)(3-\lambda)+1 =\lambda^2-4\lambda+3+1=(\lambda-2)^2=0\)
Hier uit volgt dat \(\lambda=2\) is een eigenwaarde met mutlipliciteit twee.
\(\lambda=2\): Los nu op \(\left(\mathbf{A}-2\mathbf{I} \right) \bar v_1 = \bar 0 \)
\(\left( \begin{array}{cc} -1 & -1 \\ 1 & 1 \end{array}\right)\left( \begin{array}{c} v_{1x} \\ v_{1y} \end{array}\right)=\left( \begin{array}{c} 0 \\ 0 \end{array}\right) \Leftrightarrow \left\{\begin{array}{c} -v_{1x}-v_{1y}=0 \\ v_{1x}+v_{1y}=0\end{array}\right.\)
Beide vergelijkingen geven \(v_{1x}=-v_{1y}\). We kunnen nu weer een willekeurige \(y\) coördinaat kiezen b.v \(v_{1y}=1 \Rightarrow v_{1x}=-1\). Een eigenvector is dan
\(\bar v_1 = \left( \begin{array}{c} -1 \\ 1 \end{array}\right)\)

Voor de tweede eigenvector lossen we op: \(\left(\mathbf{A}-2\mathbf{I} \right)^2 \bar v_2 = \bar 0 \)
\(\left( \begin{array}{cc} -1 & -1 \\ 1 & 1 \end{array}\right)^2\left( \begin{array}{c} v_{2x} \\ v_{2y}\end{array}\right)=\left( \begin{array}{cc} -1 & -1 \\ 1 & 1 \end{array}\right)\left( \begin{array}{cc} -1 & -1 \\ 1 & 1 \end{array}\right)\left(\begin{array}{c} v_{2x} \\ v_{2y}\end{array}\right)= \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right)\left( \begin{array}{c} v_{2x} \\ v_{2y}\end{array}\right)=\left( \begin{array}{c} 0 \\ 0 \end{array}\right) \Leftrightarrow \left\{\begin{array}{c}0v_{2x}+0v_{2y}=0 \\ 0v_{1x}+0v_{2y}=0\end{array}\right.\)
Alle combinaties \(v_{2x}\) en \(v_{2y}\) voldoen aan deze vergelijking. We moeten er alleen voor zorgen dat \(\bar v_2\) onafhankelijk is van \(\bar v_1\). Een eigenvector is dan bijvoorbeeld
\(\bar v_2 = \left( \begin{array}{c} 1 \\ 0 \end{array}\right)\)

In drie dimensies kunnen we op de zelfde manier een karakteristieke vergelijking opstellen als in twee dimensies. Namelijk door de determinant van \(\left(\mathbf{A} - \lambda \mathbf{I}\right)\) gelijk aan nul te stellen

\(\left|\mathbf{A} - \lambda \mathbf{I}\right|=\left| \begin{array}{lll} a_{11}-\lambda & a_{12} & a_{13} \\ a_{21} & a_{22}-\lambda & a_{23} \\ a_{31} & a_{32} & a_{33}-\lambda \end{array}\right|=\)

\((a_{11}-\lambda)(a_{22}-\lambda)(a_{33}-\lambda)+ a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32} -a_{13}(a_{22}-\lambda)a_{31}-(a_{11}-\lambda)a_{23}a_{32} -a_{12}a_{21}(a_{33}-\lambda) =0\)

Dit is een derdegraadsvergelijking die drie mogelijk samenvallende oplossingen heeft. Hieronder is het algemene recept te vinden voor het algebraïsch oplossen van een derdegraadsvergelijking. Voor hogeregraadsvergelijkingen zijn er geen algemene oplossingsformules. Sterker nog het is bewezen dat die er ook niet kunnen zijn. Omdat de theorie uit deze sectie toegepast wordt in de analyse van continue dynamische systemen die in de praktijk vaker in hogere dimensies worden toegepast is het nut van het recept voor derdegraadsvergelijking vrij klein.

Voorbeeld: Bepaal de eigenwaarden en eigenvectoren voor de matrix \(\mathbf{A}=\left( \begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & -1 \\ 0 & 1 & 1 \end{array}\right)\).
De karakteristieke vergelijking voor de matrix \(\mathbf{A}\) is:
\(\det(\mathbf{A}-\mathbf{I})=\left| \begin{array}{lll} 1-\lambda & 0 & 0 \\ 0 & 1-\lambda & -1 \\ 0 & 1 & 1-\lambda \end{array}\right|=(1-\lambda)(1-\lambda)(1-\lambda)-(1-\lambda)(-1)1=(1-\lambda)((1-\lambda)^2+1) =0\)
Deze vergelijking heeft als oplossingen:
\( \begin{array}{lll}(1-\lambda)=0 & \Leftrightarrow & \lambda=1 \\ & \;\vee\; & \\ (1-\lambda)^2+1 =0 & \Rightarrow & \lambda=1+i \;\vee\; \lambda=1-i \end{array}\)
\(\lambda_1=1\): De eigenvector \(\bar{v}_1\) voor deze eigenwaarde lossen we op uit
\((\mathbf{A}-\lambda\mathbf{I})\bar{v}_1=\left(\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{array}\right)\left(\begin{array}{c} v_{1x} \\ v_{1y} \\ v_{1z} \end{array}\right)=\bar0=\left(\begin{array}{c} 0 \\ 0 \\ 0 \end{array}\right) \Leftrightarrow \left\{\begin{array}{lll} 0 & = & 0 \\ -v_{1z} & = & 0 \\ v_{1y} & = & 0 \end{array}\right.\).
We mogen \(v_{1x}\) vrij kiezen. De vector \(\bar{v}_1=\left(\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right)\) is dus een eigenvector.
\(\lambda_1=1+i\): De eigenvector \(\bar{v}_2\) voor deze eigenwaarde lossen we op uit
\((\mathbf{A}-(1+i)\mathbf{I})\bar{v}_2=\left(\begin{array}{ccc} -i & 0 & 0 \\ 0 & -i & -1 \\ 0 & 1 & -i \end{array}\right)\left(\begin{array}{c} v_{2x} \\ v_{2y} \\ v_{2z} \end{array}\right)=\bar0=\left(\begin{array}{c} 0 \\ 0 \\ 0 \end{array}\right) \Leftrightarrow \left\{\begin{array}{lll} -iv_{2x} & = & 0 \\ -iv_{2y}-v_{2z} & = & 0 \\ v_{2y}-iv_{2z} & = & 0 \end{array}\right.\).
Dus \(v_{2x}=0\) en de laatste twee vergelijkingen leveren \(v_{2y}=iv_{2z}\). Kiezen we \(v_{2z}=1\) dan is de vector \(\bar{v}_2=\left(\begin{array}{c} 0 \\ i \\ 1 \end{array}\right)\) een eigenvector.
\(\lambda_1=1-i\): De eigenvector \(\bar{v}_2\) voor deze eigenwaarde lossen we op uit
\((\mathbf{A}-(1+i)\mathbf{I})\bar{v}_2=\left(\begin{array}{ccc} i & 0 & 0 \\ 0 & i & -1 \\ 0 & 1 & i \end{array}\right)\left(\begin{array}{c} v_{3x} \\ v_{3y} \\ v_{3z} \end{array}\right)=\bar0=\left(\begin{array}{c} 0 \\ 0 \\ 0 \end{array}\right) \Leftrightarrow \left\{\begin{array}{lll} iv_{3x} & = & 0 \\ iv_{3y}-v_{3z} & = & 0 \\ v_{3y}+iv_{3z} & = & 0 \end{array}\right.\).
Dus \(v_{3x}=0\) en de laatste twee vergelijkingen leveren \(v_{3y}=-iv_{3z}\). Kiezen we \(v_{3z}=1\) dan is de vector \(\bar{v}_2=\left(\begin{array}{c} 0 \\ -i \\ 1 \end{array}\right)\) een eigenvector.

Inverse matrix

Gegeven is de twee dimensionale transformatie \(A=\left(\begin{array}{cc} a & b \\ c & d \end{array}\right)\). Passen we deze tansformatie toe op \(\bar{x}\) dan krijgen we het beeld \(\bar{x}'=A\bar{x}\). Nemen we als startpunt \(\bar{x}'\) dan is er ook een transformatie die als beeld \(\bar{x}\) oplevert. Deze transformatie noemen we de inverse van \(A\) en wordt aangegeven met \(A^{-1}\). Pas je eerst \(A\) toe op \(\bar{x}\) en vervolgens \(A^{-1}\) dan ben je weer terug in de oorspronkelijke toestand dus: \(A^{-1}A\bar{x}=\bar{x}\), zodat \(A^{-1}A\) gelijk moet zijn aan de eenheidsmatrix \(I\).

De inverse matrix \(A^{-1}\) kun je uit \(A\) als volgt uit verkrijgen.

\(A^{-1}=\frac{1}{det(A)}\left(\begin{array}{cc} d & -b \\ -c & a \end{array}\right)\)

Een voorwaarde van het bestaan van \(A^{-1}\) is dat \(det(A)\) niet gelijk aan 0 mag zijn

Toon met een berekening aan dat inderdaad geldt \(A^{-1}A=I\).

Geef een meetkundige betekenis aan de voorwaarde \(det(A) \neq 0\).

Bepaal de inverse van de matrix \(\mathbf{A}=\left( \begin{array}{cc} 1 & -1 \\ 2 & 3 \end{array}\right)\).
Antwoord: \(A^{-1}=\frac{1}{1 \cdot 3- 2 \cdot (-1)}\left(\begin{array}{cc} 3 & 1 \\ -2 & 1 \end{array}\right)=\left(\begin{array}{cc} \frac{3}{5} & \frac{1}{5} \\ -\frac{2}{5} & \frac{1}{5} \end{array}\right)\)

Praktische betekenis van eigenwaarden en eigenvectoren

Stelling: Iedere vector \(\bar{x}\) in een twee dimensionale ruimte kan worden geschreven als een unieke combinatie van twee willekeurige onafhankelijke vectoren \(\bar{u}\) en \(\bar{v}\) (\(\bar{u} \neq a \cdot \bar{v}\)).

\(\bar{x}=a \cdot \bar{u} + b \cdot \bar{v}\)

In een \(n\)-dimensionale ruimte kan iedere vector \(\bar{x}\) als een combinatie van \(n\) willekeurige onafhankelijke vectoren worden geschreven.

Conclusie: Iedere vector \(\bar{x}\) in een twee dimensionale ruimte kan worden geschreven als een combinatie van de eigenvectoren \(\bar{v}_1\) en \(\bar{v}_2\) van een matrix \(A\) waarvoor \(\det(A)!=0\).

In een \(n\)-dimensionale ruimte kan iedere vector \(\bar{x}\) in als een combinatie van de \(n\) eigen vectoren van een matrix \(A\) waarvoor \(\det(A)!=0\).

Voorbeeld: Gegeven zijn de vectoren \(\bar{x}=\left(\begin{array}{c} 4 \\ 5 \end{array}\right)\), \(\bar{u}=\left(\begin{array}{c} 1 \\ 2 \end{array}\right)\) en \(\bar{v}=\left(\begin{array}{c} -1 \\ 1 \end{array}\right)\). Bepaal de waarden \(a\) en \(b\) zodat \(\bar{x}=a \cdot \bar{u} + b \cdot \bar{v}\). Oplossing:

\(\left(\begin{array}{c} 4 \\ 5 \end{array}\right)=a \cdot \bar{u}=\left(\begin{array}{c} 1 \\ 2 \end{array}\right) + b \cdot \left(\begin{array}{c} -1 \\ 1 \end{array}\right) \Leftrightarrow\)
\(\left(\begin{array}{ccc} 4&=& a - b \\ 5 &=& 2a + b \end{array}\right) \Leftrightarrow\)
\(\left(\begin{array}{ccc} 4&=& a - b \\ 9 &=& 3a \end{array}\right) \Leftrightarrow\)
\(\left(\begin{array}{ccc} -1 &=& b \\ 3 &=& a \end{array}\right)\)

Dus \(\bar{x}=3 \cdot \bar{u} - 1 \cdot \bar{v}\)

Bewijs deze stelling.

Bewijs deze conclusie.

Voorbeeld:
Bepaal de directe formule \(\bar{Q}_n\) voor de reeks \(\bar{Q}_n=A \bar{Q}_n\) met \(\bar{Q}_0=\bar{P}\) waarin \(\mathbf{A}=\left( \begin{array}{cc} 4 & -2 \\ 3 & -1 \end{array}\right)\) en \(\bar{P}=\left(\begin{array}{c} 3 \\ 4 \end{array}\right)\).
Oplossing: Merk eerst op dat het hier om een meetkundige reeks gaat. Dus \(\bar{Q}_n=A^n\bar{P}\)
De matrix is in een eerder voorbeeld geanalyseerd en heeft eigenwaarden \(\lambda_1=1\) en \(\lambda_2=2\) met eigenvectoren \(\bar v_1 = \left( \begin{array}{c} 2 \\ 3 \end{array}\right)\) en \(\bar v_2 = \left( \begin{array}{c} 1 \\ 1 \end{array}\right)\)
In dit geval is het eenvoudig in te zien dat \(\bar{P}=1 \cdot \bar{v}_1 + 1 \cdot \bar{v}_2\)
De gevraagde directe formule is dus \(\bar{Q}_n=1 \cdot 1^{n}\bar{v}_1 + 1 \cdot 2^{n} \bar{v}_2 = \left( \begin{array}{c} 2 \\ 3 \end{array}\right)+ 2^n \left( \begin{array}{c} 1 \\ 1 \end{array}\right)\)

Lineaire recurrente betrekking van de eerste orde

Gegeven is reeks \(\bar{u}_n=A\bar{u}_{n-1}+\bar{t}\), met \(\bar{u}_{0}=\bar{b}\). Voor deze reeks is er onder bepaalde voorwaarden een evenwicht. Dit evenwicht van deze reeks wordt als volgt berekend:

\(\bar{u}=A\bar{u}+\bar{t} \Rightarrow\)
\(\bar{u}-A\bar{u}=\bar{t} \Rightarrow\)
\((I-A)\bar{u}=\bar{t} \Rightarrow\)
\(\bar{u}=(I-A)^{-1}\bar{t}\).

Een evenwicht kan stabiel of niet stabiel zijn. Stabiliteit van een evenwicht betekent dat de reeks naar dit evenwicht convergeert voor als \(n\) toeneemt. Dit evenwicht is stabiel als voor alle eigenwaarden van matrix \(A\) geldt \(|\lambda| \leq 1\). Als dit niet het geval is dan is het evenwicht niet stabiel.

Bepaal het effect van de translatie in het voorbeeld in de applet.

Wanneer bestaat er geen evenwicht.

Dat de stabiliteit van het evenwicht alleen afhangt van de linaire transformatie \(A\) wordt duidelijk als we de reeks \(\bar{v}_{n}\) voor de uitwijking uit het evenwicht bekijken. Deze reeks is gelijk aan:
\(\begin{eqnarray} \bar{v}_{n}& = & \bar{u}_{n}-\bar{u}\\ & = & A\bar{u}_{n-1}+t-(A\bar{u}+t)\\ & = & A\bar{u}_{n-1}-A\bar{u}\\ & = & A(\bar{u}_{n-1}-\bar{u})\\ & = & A\bar{v}_{n-1} \\ \end{eqnarray}\) De reeks van de uitwijkingen wordt dus bepaald door de lineaire transformatie \(A\).

Beredeneer nu waarom het evenwicht stabiel is als geldt \(|\lambda| \leq 1\) voor ieder eigenwaarde van de matrix \(A\).

Voorbeeld: Gegeven is de reeks \(\bar{u}_{n} =\left( \begin{array}{cc} 0.8 & -0.3 \\ 0.3 & 0.8 \end{array}\right)\bar{u}_{n-1}+\left( \begin{array}{c}5 \\ 4 \end{array}\right)\), met \(\bar{u}_{0}=\left( \begin{array}{c} 5 \\ 5 \end{array}\right)\)
a) Bereken de waarden \(\bar{u}_{1} , \bar{u}_{2}\).
Antwoord:
\(\bar{u}_{1} =\left( \begin{array}{cc} 0.8 & -0.3 \\ 0.3 & 0.8 \end{array}\right)\left( \begin{array}{c} 5 \\ 5 \end{array}\right)+\left( \begin{array}{c}5 \\ 4 \end{array}\right)=\left( \begin{array}{c} 7.5 \\ 9.5 \end{array}\right)\)
\(\bar{u}_{2} =\left( \begin{array}{cc} 0.8 & -0.3 \\ 0.3 & 0.8 \end{array}\right)\left( \begin{array}{c} 7.5 \\ 9.5 \end{array}\right)+\left( \begin{array}{c}5 \\ 4 \end{array}\right)=\left( \begin{array}{c} 8.15 \\ 13.85 \end{array}\right)\)
b) Bereken het evenwicht van de reeks en bepaal de stabiliteit van dit evenwicht.
Antwoord:
Evenwicht:\(\bar{u}=(I-A)^{-1}\bar{t}=\left( \begin{array}{cc} 0.2 & 0.3 \\ -0.3 & 0.2 \end{array}\right)^{-1}\left( \begin{array}{c}5 \\ 4 \end{array}\right)\).
\(\left( \begin{array}{cc} 0.2 & 0.3 \\ -0.3 & 0.2 \end{array}\right)^{-1}=\frac{1}{0.4+0.9}\left( \begin{array}{cc} 0.2 & -0.3 \\ 0.3 & 0.2 \end{array}\right)\)
\(\bar{u}=\frac{1}{0.4+0.9}\left( \begin{array}{cc} 0.2 & -0.3 \\ 0.3 & 0.2 \end{array}\right)\left( \begin{array}{c}5 \\ 4 \end{array}\right)=\left( \begin{array}{c} \frac{-20}{13} \\ \frac{230}{13} \end{array}\right)\).
Stabiteit: Eigenwaarden uit \(\det(A-\lambda I)=(0.8-\lambda)^{2}+0.09=0\). De oplossingen voor deze vergelijkingen zijn \(\lambda_{1}=0.8-0.3 i\) en \(\lambda_{2}=0.8 + 0.3 i\). \(|\lambda_{1,2}|=0.73 < 1\). Dus evenwicht stabiel.