Leerdoelen
Na dit hoofdstuk:- weet je het doel en de taak van clusteranalyse bij datamining.
- kun je een paar toepassingen van clustering noemen.
- kun je de begrippen datapunt, object, cluster, centrum, centroide, Euclidische afstand, Manhattan afstand en centrum uitleggen.
- kun je de afstand tussen zowel twee objecten als twee clusters met behulp van afstandsmaten zoals Euclidische afstand en Manhattan afstand berekenen.
- kun je het centrum of de centroide van een cluster bepalen.
- ben je in staat de $K$-means methode op passende problemen toepassen
- weet je dat er ook nog andere clustermethoden zijn.
- ben je je bewust van de problemen die bij clustering op kunnen treden
Inleiding
Stel er komt een aantal buitenlandse studenten binnen op de hogeschool waar jij als studiecoördinator werkt en jij moet er voor zorgen dat deze studenten worden bijgeschoold in Engels voordat zij mogen beginnen met de rest van de opleiding.
Er zijn twee docenten beschikbaar en je wilt de studenten indelen in twee groepen (een groep noemen we in het vervolg een cluster), groep A en groep B. Bij de indeling wil je clusters maken van studenten van gelijk niveau. De grootte van de clusters is onbelangrijk.
Je wilt indelen op de twee eigenschappen lezen en verstaan van Engels. Je laat daarom alle studenten een test maken waaruit een score van 1 tot 10 komt. Daarbij geef je alleen gehele punten als cijfer.
Om inzicht te krijgen hoe je de clusters kunt indelen zet je de studenten in een schema waarbij de horizontale as het cijfer voor lezen aangeeft en de verticale as het cijfer voor verstaan. In het onderstaande schema zijn de resultaten van de vijf studenten s1 t/m s5 weergegeven.

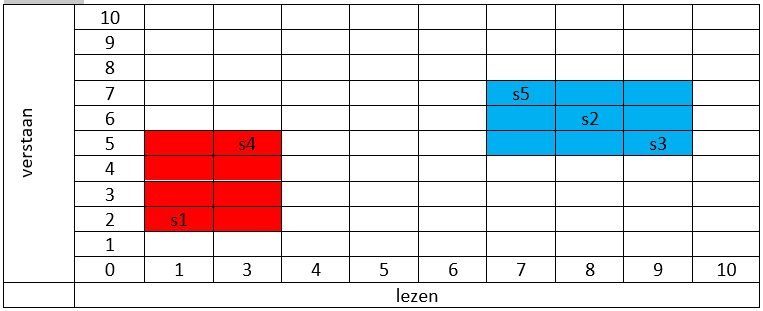
De meest logische indeling is om s1 en s4 in groep A te stoppen en s2,s3 en s5 in groep B.
In het voorbeeld was het niet zo moeilijk om te bepalen welke clusters je het best kon maken. Maar wat nu als er veel meer studenten zijn en/of veel meer eigenschappen zijn waar je rekening mee wilt houden?
Clusteranalyse is het classificeren of het groeperen in 'clusters' of 'klassen' van objecten op grond van hun kenmerken zonder vooraf de clusters vast te leggen. De gebruikte algoritmen bepalen wel de weg om tot clusters te komen, maar de gegevens bepalen welke clusters het worden. Deze algoritmen zijn, net als de algoritmen uit de associatie analyse, vormen van unsupervised learning (= ongestuurd leren). Het belangrijkste AI-kenmerk is ook hier: de invoer die het programma krijgt, is niet volledig te bepalen en is complex.
- Wat zijn in het voorbeeld de objecten en de kenmerken?
antwoord
- De objecten zijn de studenten, de kenmerken de resultaten voor lezen en verstaan.
van objecten
Het doel van clusteranalyse (trainingsfase) is het vormen van deelverzamelingen (clusters of groepen) die elk hun eigen gedeelde kenmerken bevatten. De clusters en liefst ook het aantal clusters zijn vooraf niet bekend. Het streven is zoveel mogelijk gelijkenis binnen een groep en zoveel mogelijk verschil tussen de groepen te krijgen.
De clusteranalyse levert een aantal groepen, de clusters, op. Op basis van die groepen kun je bepalen tot welke groep een aan de applicatie aangeboden object behoort. In het voorbeeld van de studenten waren er al twee klassen gemaakt, een nieuwe student wordt dan toegevoegd aan de best passende klas. Een ander voorbeeld zou kunnen zijn dat jij films krijgt aangeboden nadat jij een aantal wensen hebt aangegeven op een website. Van te voren is er al een classificatie van films gemaakt en jij krijgt dan die films voorgeschoteld die in het cluster zitten dat het best bij jouw wensen past.
Men zou ook dit aangeboden object aan de trainingsdata kunnen toevoegen en de clusteranalyse opnieuw uitvoeren. Dit zou kunnen leiden tot een nieuwe groepsindeling. We gaan het hier vooral over de trainingsfase hebben: het algoritme K-means-clustering.
Voor we het algoritme ($K$-means-clustering) meer in detail uitwerken en jullie laten kennismaken met alternatieve clusteralgoritmen geven we eerst een aantal voorbeelden van terreinen waarin clusteranalyse wordt toegepast. Meer voorbeelden zijn onder andere hier en hier te vinden.
Toepassingen
- Identificatie van nepnieuws
Nepnieuws is geen nieuw fenomeen, maar het treedt meer en meer op de voorgrond vooral binnen sociale media. Zelfs president Trump schaamde zich niet om zijn campagne met nepnieuws te voeren of ander onwelgevallige berichten tot nepnieuws te bombarderen.
In een artikel gepubliceerd door twee informaticastudenten (Seyedmehdi Hosseinimotlagh en Evangelos E. Papalexakis, University of California, Riverside) wordt een clusteralgoritme gebruikt om nepnieuws te identificeren. Het algoritme krijgt (nep)nieuwsartikelen aangeboden. Uit deze artikelen worden de belangrijkste en meest sensatierijke woorden gevist. Op deze woorden wordt dan geclusterd. Omdat sensatiebeluste woorden de aandacht van mensen trekken komen deze woorden vaker voor in nepnieuwsartikelen. De clusters bevatten dus combinaties van dit soort woorden waarmee nieuwe berichten geclassificeerd kunnen worden op mate van nepnieuws.
- Biologie
- In de biologie zijn er meerdere gebieden waar clusteranalyse wordt toegepast. Denk bijvoorbeeld aan de classificatie van verschillende organismen. Elk organisme hoort bij een soort. Soorten kunnen op hun beurt weer worden onderverdeeld in lagere taxa, zoals ondersoort en variëteit. Soorten zelf worden samengevoegd in geslachten en deze weer in families en in taxa van nog hogere rang. Een ander voorbeeld van het gebruiken clustertechnieken in de biologie is het maken van groepen met genen die een bepaalde erfelijke ziekte kunnen bevatten. Door het gebruik van clustermethoden kunnen groepen met samenwerkende genen gevonden worden. Als deze groepen bekend zijn, kan deze kennis helpen om meer gericht onderzoek te doen naar medicijnen die een erfelijke ziekte gekoppeld aan de groep genen kan voorkomen of genezen.
- Marketing
- Personalisatie en bepaling van doelgroepen in marketing is big business. Dit wordt bereikt door naar specifieke kenmerken van een persoon te kijken en campagnes met hen te delen die succesvol zijn geweest met andere vergelijkbare mensen. Doet een bedrijf dat niet of verkeerd dan loopt het bedrijf de kans niets te verkopen of nog erger het vertrouwen van klanten te verliezen. Clusteranalyse helpt de doelgroepen te bepalen.
Clusters en afstanden
Om verder te kunnen met de clusteranalyse, hebben we extra begrippen nodig. Het gaat vooral om het begrip 'afstand'. Hoe meet je nu precies of twee objecten met hun eigenschappen dicht bij elkaar liggen?
Afstandsmaten
In clustering speelt afstand tussen gegevens een grote rol. Een computer heeft daar meestal getallen voor nodig. Vaak moet er eerst een bewerking van gegevens plaatsvinden om deze om te zetten in getallen. Combinatie van verschillende eigenschappen leveren dan datapunten op in een assenstelsel. Iedere eigenschap heeft dan zijn eigen as, bijvoorbeeld leeftijd, sociale klasse, salaris...
Afstand tussen datapunten (objecten):
Wat is de afstand tussen $s_{1}$ en $s_{4}$?
- De kortste afstand tussen $s_{1}$ en $s_{4}$ is $\sqrt{13}$. Weet je hoe je die afstand berekent?
Als je alleen langs de roosterlijnen mag meten dan is de kortste afstand 5. Het is dus van belang eerst een lengtemaat vast te leggen.

Je kunt alleen over de weg.
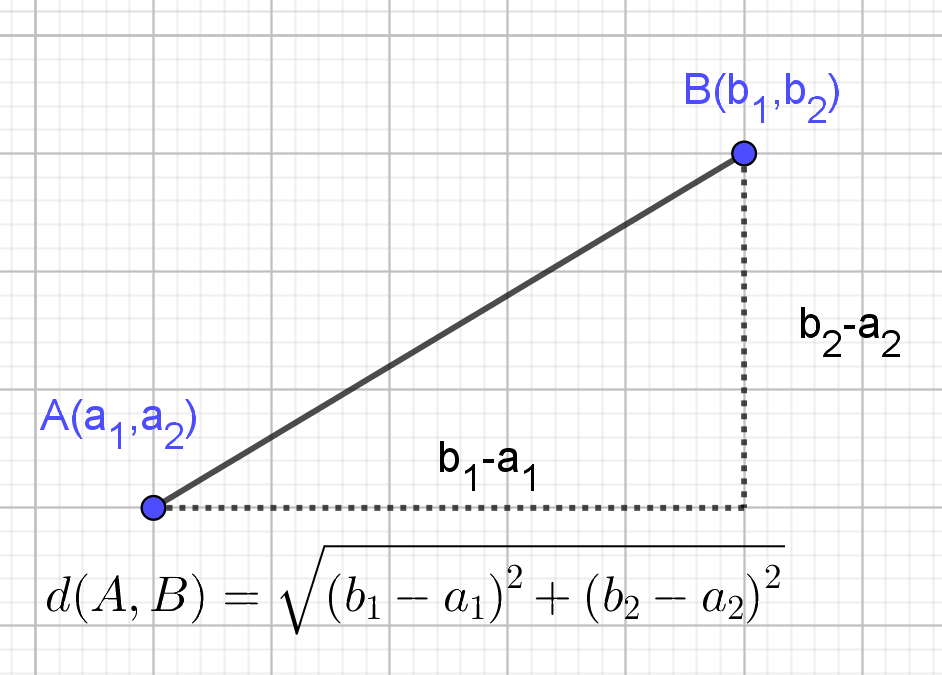
Hebben we datapunten zoals hierboven dan kunnen we wiskundig de afstand tussen punten uitrekenen. Je hebt waarschijnlijk de vorige vraag beantwoord met de stelling van Pythagoras. De stelling van Pythagoras (Figuur 2) is de manier om de afstand van de schuine zijde in een tweedimensionale rechthoekige driehoek te berekenen. In een assenstelsel vormen de verplaatsingen langs de assen de rechthoekzijden en de lengte van schuine zijde de kortste afstand tussen de punten. Deze afstand noemt men ook wel de Euclidische afstand,ook wel de vogelvluchtafstand. In drie dimensies en hoger wordt op een zelfde manier de afstand tussen twee punten berekend.
Naast de Euclidische afstand is er een andere maat die vaak gebruikt wordt, de Manhattan of City-block afstand. In figuur 3 zie je een stukje van de kaart van Manhattan. Je kunt alleen van hoek naar hoek komen als je door de straten gaat. Schuin, dwars door een blok, zoals bij de Euclidische afstand, is onmogelijk. In een rooster kun je dus alleen evenwijdig aan de assen bewegen.
Afstandsmatrix
Een matrix van afstanden is een matrix waarvan de elementen de afstanden tussen de punten aangeven.
Afstand tussen clusters
Als je de afstand tussen elk paar van objecten weet, wat is dan de
afstand tussen twee clusters $C_{1}$ en $C_{2}$?
We nemen hier de kleinste afstand tussen twee objecten waarvan er één
in $C_{1}$ aanwezig is en de andere in $C_{2}$. Deze afstand noemt men
Single Linkage.
Centrum cluster
Als we straks na de training clusters hebben gevormd en willen bepalen in welk cluster een nieuw object moet worden geplaatst is het heel efficiënt om een cluster op een bepaalde manier samen te vatten. Het centrum $M(m_{1},m_{2}, \dots, m_{n})$ van een cluster bestaande uit $k$ punten wordt die samenvatting. Het centrum is een punt $M$ met $n$ coördinaten $m_{1},m_{2}, \dots, m_{n}$ en wordt berekend door het gemiddelde te nemen van al de coördinaten van de punten in de cluster. Wiskundig gezien is het centrum het zwaartepunt van de veelhoek ( een lichaam in hogere dimensie) die door de punten wordt gevormd.
Cluster methoden
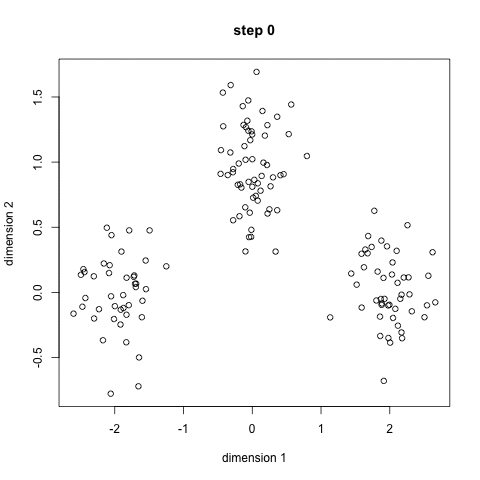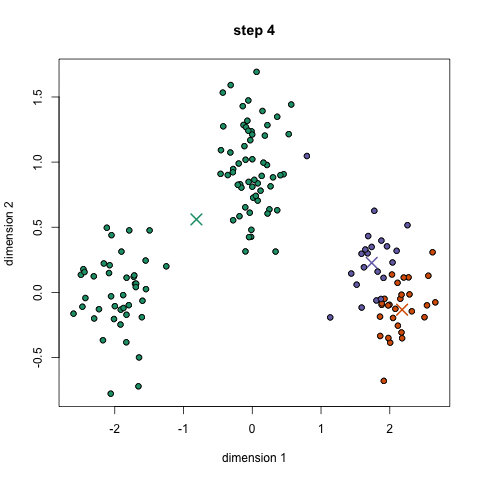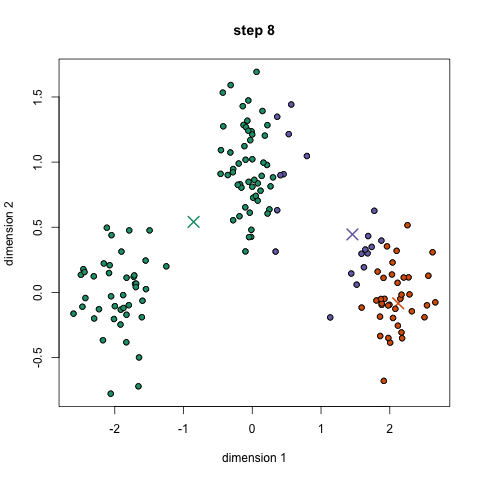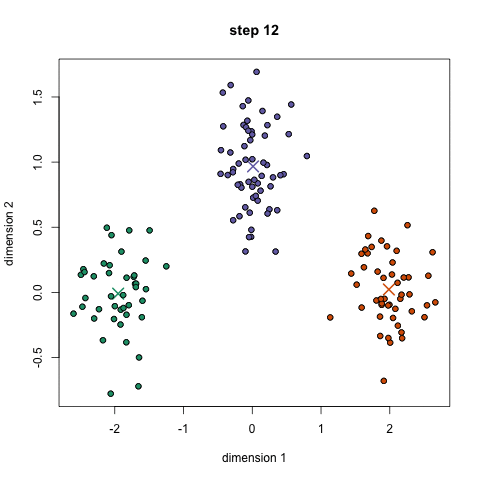
Er zijn verschillende methoden die gebruikt worden om tot clusters te komen. We presenteren hier $K$-means-clustering. In figuur 4 zie je een animatie van de werking, waarbij de data stap voor stap in drie groepen wordt verdeeld. De kleuren geven de clusters aan en de kruisjes die je ziet bewegen zijn de centra van de clusters.
$K$-means-clustering
K-means clustering is een eenvoudige en relatief snelle iteratieve manier van clusteren. Het is het oudste en meest bekende clusteralgoritme. Later zijn er veel varianten van deze methode ontwikkeld die het clusteren weer net wat sneller, slimmer aanpakken. Het gaat te ver om die hier te bekijken.
Voorafgaande aan het clusteren wordt bepaald hoeveel clusters ( b.v. $k$=3 ) je wilt krijgen. De clustering (training) op basis van de gegevens levert dan die clusters die worden samengevat door de bijbehorende centra. Het algoritme meet veel afstanden, we passen het daarom toe op punten in het platte vlak, zodat je met pen, papier en liniaal eenvoudig het algoritme na kan spelen.
In figuur 5 staat de flowchart van het algoritme dat we hieronder in meer detail beschouwen.
Om de optimale clustering te vinden ga je als volgt te werk:
- Start: Kies de centra van de clusters de eerste keer willekeurig en bepaal het maximaal aantal stappen dat je toestaat.
- Daarna bepaal je van elk datapunt de afstand tot ieder centrum, en wijs je ieder datapunt toe aan de cluster waarvan het centrum het meest dichtstbij is.
- Als er punten zijn die in de vorige stap van cluster zijn veranderden je nog niet voorbij het vooraf gekozen maximum aantal iteraties bent gekomen dan ga je naar stap 3. Anders ben je klaar.
- Alle datapunten zitten weer in een cluster. Er zijn datapunten
die nu in een andere cluster zitten. De centra zijn dan niet voor
alle clusters meer hetzelfde en moeten dus opnieuw worden berekend. Hiervoor gebruik je voor ieder
cluster apart de volgende formule:
$M(m_{1},m_{2}, \dots, m_{n})= \left( \frac{\sum^{1}_{n} a_{1i}}{n},\frac{\sum^{1}_{n} a_{2i}}{n}, \dots, \frac{\sum^{1}_{n} a_{ni}}{n}\right)$.
$n$ is dan het aantal elementen in één cluster.
Met die nieuwe centra veranderen ook weer de afstanden van de datapunten tot die centra en moet je dus het hele proces vanaf stap 2 weer herhalen, ofwel start de volgende iteratie.
Bij stap 1 in het algoritme zijn nog twee opmerkingen nodig. Om te beginnen de keuze van de startpunten voor de centra. Die is willekeurig, maar ze moeten wel een beetje in de buurt van de objecten liggen. Als een cluster leeg blijft kan het algoritme niet goed werken, het geeft zelfs een fout. Een simpele keuze is gewoon een paar punten uit de lijst van objecten te nemen.
Ten tweede is er het aantal iteraties. Bij grote puntenwolken kan het algoritme heel lang doorgaan, waarbij steeds minder punten van cluster wisselen. Er verandert dan op den duur weinig meer en je kunt net zo goed stoppen. Wat ook kan optreden is dat een object in een oneindige herhaling per iteratie van cluster wisselt. Om dergelijke problemen te voorkomen kun je een maximaal aantal iteraties opgeven.
Vragen
K-means
| Geef aantal clusters | |
| Geef objecten lijst in javascript format | |
| Geef lijst begin centra |
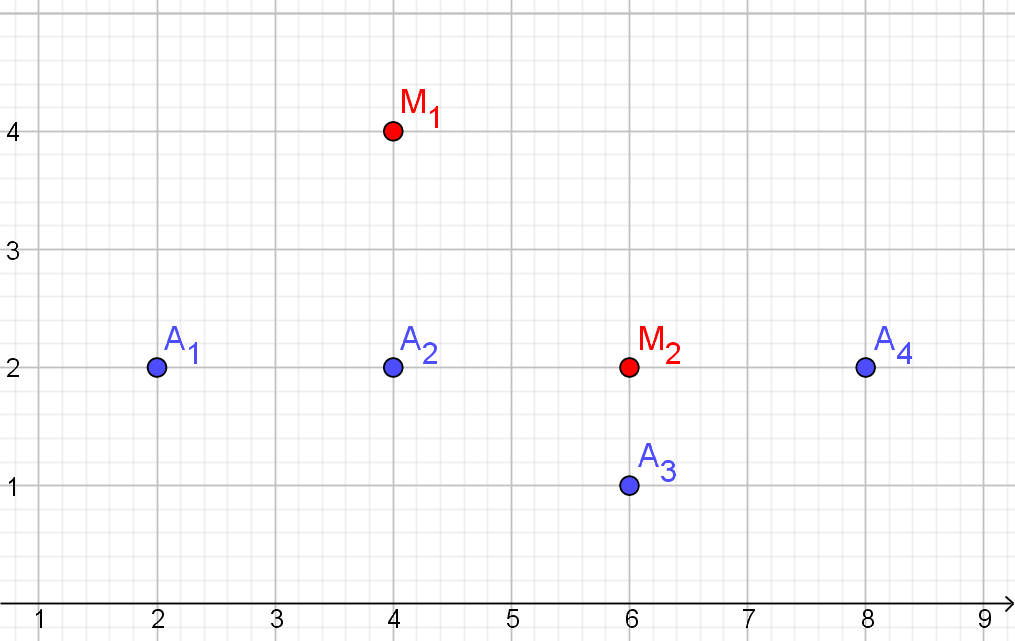
- Gegeven is een dataset met 6 datapunten.
Als afstandsmaat gebruiken we de normale (Euclidische) afstand.$x_{1}$ $x_{2}$ $x_{3}$ $x_{4}$ $A_{1}$ 6 3 4 5 $A_{2}$ 2 3 5 4 $A_{3}$ 5 4 6 3 $A_{4}$ 9 1 1 8 $A_{5}$ 8 2 0 9 $A_{6}$ 8 0 1 8 - Bereken de Euclidische afstand van $A_{1}$ en $A_{2}$
antwoord
- $d(A_{1},A_{2})=\sqrt{(6-2)^{2}+(3-3)^{2}+(4-5)^{2}+(5-4)^{2}}=\sqrt{18}=3\sqrt{2}$
- Vul de volgende afstandsmatrix in:
$A_{4}$ $A_{5}$ $A_{6}$ $A_{1}$ $A_{2}$ $A_{3}$ antwoord$A_{4}$ $A_{5}$ $A_{6}$ $A_{1}$ 5.57 6.08 5.57 $A_{2}$ 9.22 9.33 8.77 $A_{3}$ 8.66 9.22 8.66
- Bereken de Euclidische afstand van $A_{1}$ en $A_{2}$
-
Geef de afstand tussen de clusters $C_{1}$ en $C_{2}$.
antwoord
- De afstand tussen $C_{1}$ en $C_{2}$ is de kleinste afstand in de tabel dus: $d(C_{1},C_{2})=5.57$
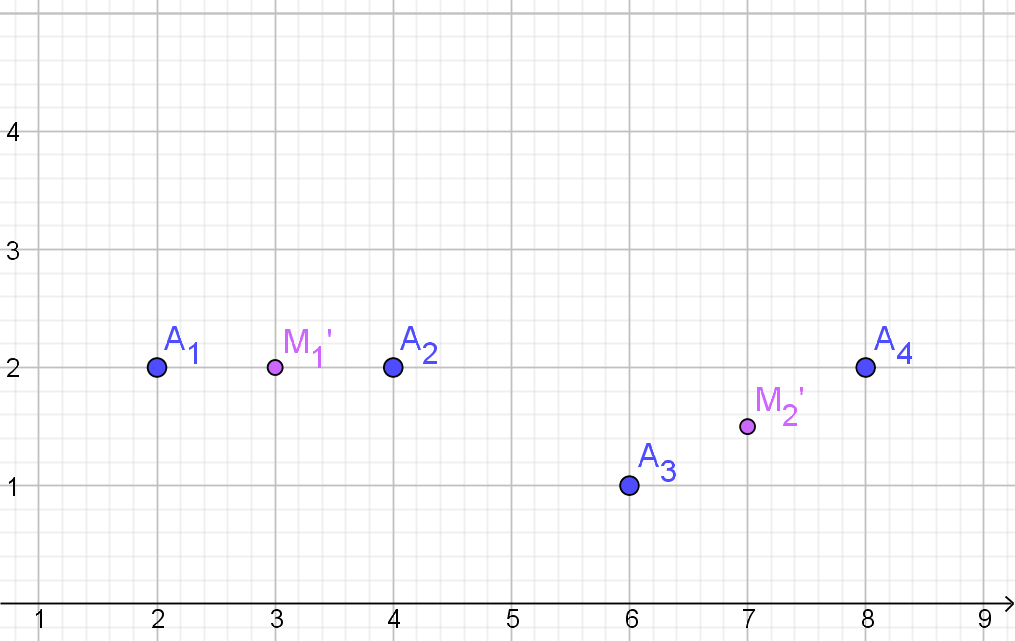
- Bereken de centra van clusters $C_{1}$ en $C_{2}$
antwoord
- $C_{1}$: centrum $M_{1}=(4.33,3.33,5,4)$
$C_{2}$: centrum $M_{2}=(8.33,1,0.67,8.33)$
- $C_{1}$: centrum $M_{1}=(4.33,3.33,5,4)$
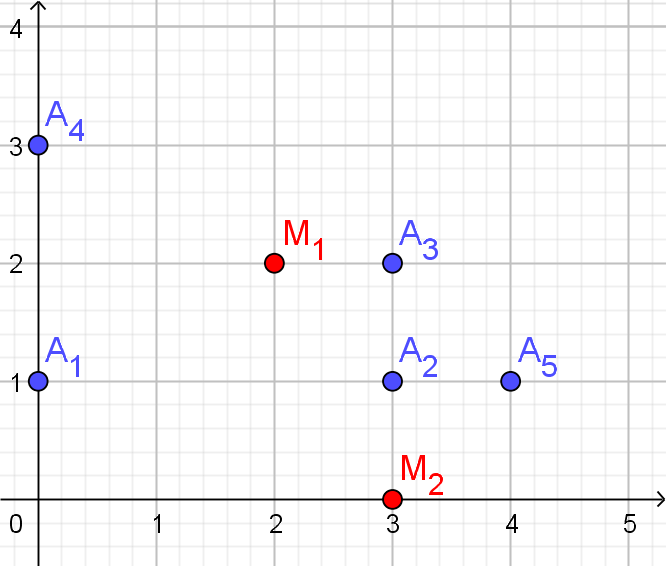
| $x_{1}$ | $x_{2}$ | |
|---|---|---|
| $O_{1}$ | 2 | 2 |
| $O_{2}$ | 8 | 6 |
| $O_{3}$ | 6 | 8 |
| $O_{4}$ | 2 | 4 |
We willen deze gegevens clusteren in twee clusters ($K$=2), met behulp van het $K$-means algoritme.
Initialiseer het algoritme met: objecten 1 en 3 in één cluster $C_{1}$ en objecten 2 en 4 in de andere cluster $C_{2}$.
Noteer $C_{1}=\{O_{1},O_{3}\}$ en $C_{2}=\{O_{2},O_{4}\}$
- Bereken het centrum $M_{1}$ van $C_{1}$ en het centrum $M_{2}$ van $C_{2}$
antwoord
- $C_{1}$: centrum $M_{1}=(4,5)$
$C_{2}$: centrum $M_{2}=(5,5)$
- $C_{1}$: centrum $M_{1}=(4,5)$
- Vul de volgende afstandsmatrix in en bereken daarmee
de afstand tussen clusters $C_{1}$ en $C_{2}$
$O_{2}$ $O_{4}$ $O_{1}$ $O_{3}$ antwoord
Dus de afstand $d(C_{1},C_{2})=2$$O_{2}$ $O_{4}$ $O_{1}$ 7.21 2 $O_{3}$ 2.83 5.7
- Bereken de afstanden tot de centra $M_{1}$ en $M_{2}$ en vul de volgende tabel in:
$M_{1}$ $M_{2}$ toewijzing $O_{1}$ $O_{2}$ $O_{3}$ $O_{4}$ antwoord$M_{1}$ $M_{2}$ toewijzing $O_{1}$ 3.6 4.2 $C_{1}$ $O_{2}$ 3.6 3.2 $C_{2}$ $O_{3}$ 4.1 3.2 $C_{2}$ $O_{4}$ 2.2 3.2 $C_{1}$
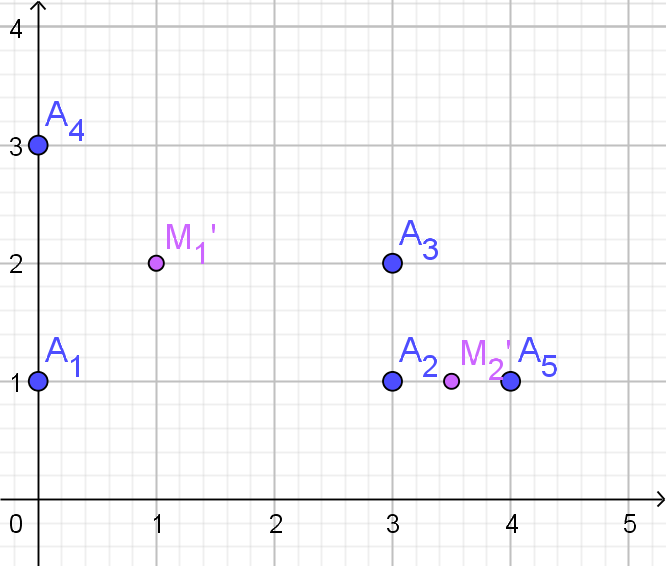
- Wat zijn uiteindelijk de clusters van het $K$-means algoritme.
antwoord
- $C_{1}=\{O_{1},O_{4}\}$ en $C_{2}=\{O_{2},O_{3}\}$
$C_{1}$: centrum $M_{1}'=\{2,3\}$
$C_{2}$: centrum $M_{2}'=\{7,7\}$
Er is geen verandering in de clustering.$M_{1}'$ $M_{2}'$ toewijzing $O_{1}$ 1 7.1 $C_{1}$ $O_{2}$ 6.7 1.4 $C_{2}$ $O_{3}$ 6.4 1.4 $C_{2}$ $O_{4}$ 1 5.8 $C_{1}$
Dus:$C_{1}=\{O_{1},O_{4}\}$ en $C_{2}=\{O_{2},O_{3}\}$
- $C_{1}=\{O_{1},O_{4}\}$ en $C_{2}=\{O_{2},O_{3}\}$
$C_{1}$: centrum $M_{1}'=\{2,3\}$
| $x_{1}$ | $x_{2}$ | |
|---|---|---|
| $D_{1}$ | 6 | 3 |
| $D_{2}$ | 2 | 3 |
| $D_{3}$ | 5 | 4 |
| $D_{4}$ | 9 | 1 |
| $D_{5}$ | 8 | 2 |
| $D_{6}$ | 8 | 0 |
We willen deze gegevens clusteren in drie clusters ($K$=3), met behulp van het $K$-means algoritme.
Initialiseer het algoritme met $C_{1}=\{D_{1},D_{2}\}$ , $C_{2}=\{D_{3},D_{4}\}$ en $C_{3}=\{D_{5},D_{6}\}$
- Bereken het centrum $M_{1}$ van $C_{1}$,
het centrum $M_{2}$ van $C_{2}$
en het centrum $M_{3}$ van $C_{3}$
antwoord
- $C_{1}$: centrum $M_{1}=(4,3)$
$C_{2}$: centrum $M_{2}=(7,2.5)$
$C_{3}$: centrum $M_{3}=(8,1)$
- $C_{1}$: centrum $M_{1}=(4,3)$
- Bereken de afstanden van de datapunten tot de centra $M_{1}$, $M_{2}$ en $M_{3}$ en vul de volgende tabel in en voer zo nodig een herclustering uit:
$M_{1}$ $M_{2}$ $M_{3}$ toewijzing $D_{1}$ $D_{2}$ $D_{3}$ $D_{4}$ $D_{5}$ $D_{6}$ antwoord-
Er is de herclustering $C_{1}=\{D_{2},D_{3}\}$ , $C_{2}=\{D_{1}\}$ en $C_{3}=\{D_{4},D_{5},D_{6}\}$$M_{1}$ $M_{2}$ $M_{3}$ toewijzing $D_{1}$ 2 1.1 2.83 $C_{2}$ $D_{2}$ 2 5.0 6.3 $C_{1}$ $D_{3}$ 1.4 2.5 4.2 $C_{1}$ $D_{4}$ 5.4 2.5 1 $C_{3}$ $D_{5}$ 4.1 1.1 1 $C_{3}$ $D_{6}$ 5 2.7 1 $C_{3}$
-
- Wat zijn de nieuwe centra en zijn we nu klaar?
antwoord
- $C_{1}=\{D_{2},D_{3}\}$ , $C_{2}=\{D_{1}\}$ en $C_{3}=\{D_{4},D_{5},D_{6}\}$
$C_{1}$: centrum $M_{1}'=(3.5,3.5)$
$C_{2}$: centrum $M_{2}'=(6,3)$ $C_{3}$: centrum $M_{3}'=(8.3,1)$
Er is weer verandering in de clustering.$M_{1}'$ $M_{2}'$ $M_{3}'$ toewijzing $D_{1}$ 2.5 0 3 $C_{2}$ $D_{2}$ 1.6 4 6.6 $C_{1}$ $D_{3}$ 1.6 1.4 4.5 $C_{2}$ $D_{4}$ 6 3.6 0.7 $C_{3}$ $D_{5}$ 4.77 2.27 1.1 $C_{3}$ $D_{6}$ 5.7 3.6 1.1 $C_{3}$
Dus:$C_{1}=\{D_{2}\}$ , $C_{2}=\{D_{1},D_{3}\}$ en $C_{3}=\{D_{4},D_{5},D_{6}\}$
Er is dus minstens nog een iteratie nodig.
- $C_{1}=\{D_{2},D_{3}\}$ , $C_{2}=\{D_{1}\}$ en $C_{3}=\{D_{4},D_{5},D_{6}\}$
| $x_{1}$ | $x_{2}$ | |
|---|---|---|
| $A_{1}$ | 0 | 0 |
| $A_{2}$ | 7 | 8 |
| $A_{3}$ | 4 | 8 |
| $A_{4}$ | 3 | 0 |
Cluster de gegevens volledig in twee clusters ($K$=2), met behulp van het $K$-means algoritme.
Initialiseer het algoritme met de willekeurige centrum $M_{1}=(0,6)$ en $M_{2}=(7,2)$. Vul je resultaten in onderstaande tabel in.
| Clusters | Centra | |
|---|---|---|
| Start | $M_{1}=(0,6)$ $M_{2}=(7,2)$ |
|
| Iteratie 1 | $C_{1}=$ $C_{2}=$ | $M_{1}=$ $M_{2}=$ |
| Iteratie 2 | $C_{1}=$ $C_{2}=$ | $M_{1}=$ $M_{2}=$ |
| ... |
- Iteratie 1:
$M_{1}$ $M_{2}$ toewijzing $A_{1}$ 6.00 7.28 $C_{1}$ $A_{2}$ 7.28 6.00 $C_{2}$ $A_{3}$ 4.47 6.71 $C_{1}$ $A_{4}$ 6.71 4.47 $C_{2}$
Iteratie 2:Clusters Centra Start $M_{1}=(0,6)$
$M_{2}=(7,2)$Iteratie 1 $C_{1}=\{A_{1},A_{3}\}$
$C_{2}=\{A_{2},A_{4}\}$$M_{1}=(2,4)$
$M_{2}=(5,4)$$M_{1}$ $M_{2}$ toewijzing $A_{1}$ 4.47 6.40 $C_{1}$ $A_{2}$ 6.40 4.47 $C_{2}$ $A_{3}$ 4.47 4.12 $C_{2}$ $A_{4}$ 4.12 4.47 $C_{1}$
Iteratie 3:Clusters Centra Start $M_{1}=(0,6)$
$M_{2}=(7,2)$Iteratie 1 $C_{1}=\{A_{1},A_{3}\}$
$C_{2}=\{A_{2},A_{4}\}$$M_{1}=(2,4)$
$M_{2}=(5,4)$Iteratie 2 $C_{1}=\{A_{1},A_{4}\}$
$C_{2}=\{A_{2},A_{3}\}$$M_{1}=(1.5,0)$
$M_{2}=(5.5,8)$
Geen verandering clustering dus klaar.$M_{1}$ $M_{2}$ toewijzing $A_{1}$ 1.50 9.71 $C_{1}$ $A_{2}$ 9.71 1.50 $C_{2}$ $A_{3}$ 8.38 1.50 $C_{2}$ $A_{4}$ 1.50 8.38 $C_{1}$
| Leeftijd | Duur vakantie | |
|---|---|---|
| $TO_{1}$ | 19 | 3 |
| $TO_{2}$ | 25 | 8 |
| $TO_{3}$ | 43 | 14 |
| $TO_{4}$ | 61 | 14 |
| $TO_{5}$ | 30 | 7 |
| $TO_{6}$ | 22 | 10 |
Cluster de gegevens volledig in twee clusters ($K$=2), met behulp van het $K$-means algoritme.
Initialiseer het algoritme met de cetra $M_{1}=TO_{1}$ en $M_{2}=TO_{2}$. Vul je resultaten in onderstaande tabel in.
| Clusters | Centra | |
|---|---|---|
| Start | $M_{1}=(19,3)$ $M_{2}=(25,8)$ |
|
| Iteratie 1 | $C_{1}=$ $C_{2}=$ | $M_{1}=$ $M_{2}=$ |
| Iteratie 2 | $C_{1}=$ $C_{2}=$ | $M_{1}=$ $M_{2}=$ |
| ... |
- Iteratie 1:
$TO_{1}$ 0.00 7.81 $C_{1}$ $TO_{2}$ 7.81 0.00 $C_{2}$ $TO_{3}$ 26.40 18.97 $C_{2}$ $TO_{4}$ 43.42 36.50 $C_{2}$ $TO_{5}$ 11.70 5.10 $C_{2}$ $TO_{6}$ 7.62 3.61 $C_{2}$
Iteratie 2:Clusters Centra Start $M_{1}=(19,3)$
$M_{2}=(25,8)$Iteratie 1 $C_{1}=\{TO_{1}\}$
$C_{2}=\{TO_{2},TO_{3},TO_{4},TO_{5},TO_{6}\}$$M_{1}=(19,3)$
$M_{2}=(36.2,10.6)$$M_{1}$ $M_{2}$ toewijzing $TO_{1}$ 0.00 18.80 $C_{1}$ $TO_{2}$ 7.81 11.50 $C_{1}$ $TO_{3}$ 26.40 7.60 $C_{2}$ $TO_{4}$ 43.42 25.03 $C_{2}$ $TO_{5}$ 11.70 7.17 $C_{2}$ $TO_{6}$ 7.62 14.21 $C_{1}$
Iteratie 3:Clusters Centra Start $M_{1}=(0,6)$
$M_{2}=(7,2)$Iteratie 1 $C_{1}=\{TO_{1}\}$
$C_{2}=\{TO_{2},TO_{3},TO_{4},TO_{5},TO_{6}\}$$M_{1}=(19,3)$
$M_{2}=(36.2,10.6)$Iteratie 2 $C_{1}=\{TO_{1},TO_{2},TO_{6}\}$
$C_{2}=\{TO_{3},TO_{4},TO_{5}\}$$M_{1}=(22,7)$
$M_{2}=(44.7,11.7)$$M_{1}$ $M_{2}$ toewijzing $TO_{1}$ 5.00 27.09 $C_{1}$ $TO_{2}$ 3.16 20.01 $C_{1}$ $TO_{3}$ 22.14 2.87 $C_{2}$ $TO_{4}$ 39.62 16.50 $C_{2}$ $TO_{5}$ 8.00 15.39 $C_{1}$ $TO_{6}$ 3.00 22.73 $C_{1}$
Iteratie 4:Clusters Centra Start $M_{1}=(0,6)$
$M_{2}=(7,2)$Iteratie 1 $C_{1}=\{TO_{1}\}$
$C_{2}=\{TO_{2},TO_{3},TO_{4},TO_{5},TO_{6}\}$$M_{1}=(19,3)$
$M_{2}=(36.2,10.6)$Iteratie 2 $C_{1}=\{TO_{1},TO_{2},TO_{6}\}$
$C_{2}=\{TO_{3},TO_{4},TO_{5}\}$$M_{1}=(22,7)$
$M_{2}=(44.7,11.7)$Iteratie 3 $C_{1}=\{TO_{1},TO_{2},TO_{5},TO_{6}\}$
$C_{2}=\{TO_{3},TO_{4}\}$$M_{1}=(24,7)$
$M_{2}=(52,14)$
Geen verandering in clusters dus klaar.$M_{1}$ $M_{2}$ toewijzing $TO_{1}$ 6.40 34.79 $C_{1}$ $TO_{2}$ 1.41 27.66 $C_{1}$ $TO_{3}$ 20.25 9.00 $C_{2}$ $TO_{4}$ 37.66 9.00 $C_{2}$ $TO_{5}$ 6.00 23.09 $C_{1}$ $TO_{6}$ 3.61 30.27 $C_{1}$
We willen deze objecten clusteren, wat we kunnen doen door middel van de $K$-means methode. Kies $K=2$, en als initiële willekeurige cluster centra: $M_{1}=(0.6,1,0)$ en $M_{2}=(7.2,1,0)$. Pas de $K$-means methode toe op $D$ tot een maximum van 3 stappen. Noteer voor elke iteratie welke clusters gevormd worden en wat de centra zijn.
Convergeert de methode? Zo ja, leg uit.
Vul de resultaten in de onderstaande tabel in:
| Clusters | Centra | |
|---|---|---|
| Start | $M_{1}=(0.6,1,0)$ $M_{2}=(7.2,1,0)$ |
|
| Iteratie 1 | $C_{1}=$ $C_{2}=$ | $M_{1}=$ $M_{2}=$ |
| Iteratie 2 | $C_{1}=$ $C_{2}=$ | $M_{1}=$ $M_{2}=$ |
| ... |
- Iteratie 1 :
$M_{1}$ $M_{2}$ toewijzing $S_{1}$ 1.54 7.34 $C_{1}$ $S_{2}$ 7.34 1.54 $C_{2}$ $S_{3}$ 4.43 2.79 $C_{2}$ $S_{4}$ 2.79 4.43 $C_{1}$
Iteratie 2:Clusters Centra Start $M_{1}=(0.6,1,0)$
$M_{2}=(7.2,1,0)$Iteratie 1 $C_{1}=\{S_{1},S{4}\}$
$C_{2}=\{S_{2},S{3}\}$$M_{1}=(1.5,0,1)$
$M_{2}=((6.3,2,1)$
Geen verandering in clusters dus klaar.$M_{1}$ $M_{2}$ toewijzing $S_{1}$ 1.50 6.61 $C_{1}$ $S_{2}$ 6.61 1.50 $C_{2}$ $S_{3}$ 3.86 1.50 $C_{2}$ $S_{4}$ 1.50 3.86 $C_{1}$
Andere cluster methoden
Als het $K$-means algoritme zo eenvoudig en snel is, waarom zijn er dan, zoals eerder genoemd, andere clusteralgoritmen? Het antwoord hierop is dat er dataverzamelingen zijn die niet passen bij het $K$-means algoritme. Bekijk maar eens het volgende plaatje.

Figuur 6: Verschillende verdelingen datapunten (bron ) en algoritmen.
De eerste kolom hoort bij een $K$-means variant. Alleen de verdeling in de vijfde rij past daar echt goed bij. Welk algoritme denk jij dat bij de verschillende rijen het beste past? Er zijn een aantal algoritmen die bij meerdere verdelingen goed scoren, maar die hebben weer andere minpunten. Het is dus van belang om te controleren of je de juiste versie kiest. Heb je meer dan twee assen dan wordt een visuele inspectie zoals in de figuur al een stuk lastiger.
De clusteralgoritmen kunnen worden onderverdeeld in partitiemethoden en hiërarchische methoden. In de partitiemethoden staat clustering met een centrum centraal. Het $K$-means valt in deze groep. In de hiërarchische methoden zijn naaste buren belangrijker. Deze buren vormen dan een stamboom vergelijkbaar met een indeling in het dierenrijk. Iedere splitsing vormt op dat niveau een cluster. In figuur 6 is Agglomerative Clustering daarvan een voorbeeld.
Voor een eerste kennismaking met clustering is het voldoende te weten dat er verschillende methoden zijn en dat deze allen iteratief werken en op afstandsmaten zijn gebaseerd. Wil je je in deze cursus meer verdiepen in clustering dan zijn de verdiepingsopdrachten hieronder een startpunt.
Vragen en opdrachten andere methoden
- Vraag: Wat is het verschil tussen hiërarchische methoden en partitiemethoden?
antwoord
- In hiërarchische wordt een stamboom gevormd op basis van nabijheid tot omliggende punten, bij partitiemethoden worden puntenverzamelingen gevormd op basis van afstand tot centra van de die puntenverzamelingen.
- Ga naar de site educlust. Er worden hier verschillende
clustermethoden aangeboden en verschillende datasets vergelijkbaar met
figuur 6. Van iedere methode wordt het algoritme getoond.
- Kies methode "k-means" en kies de dataset "Three circles sparse" en zet k op 3. Druk op de het zwarte knopje. Hoeveel iteraties zijn er gemaakt om tot het resultaat te komen? Ben je tevreden over het resultaat?
- Kies weer de methode "k-means" en kies de dataset "Three equal circles" en zet k op 3. Druk op de het zwarte knopje. Hoeveel iteraties zijn er gemaakt om tot het resultaat te komen? Ben je tevreden over het resultaat?
- Kies de hiërarchische methode "Single linkage" en kies de dataset "Three circles sparse". Druk op de het zwarte knopje. Aan het eind van het proces
hebben alle punten een gelijke kleur. Onder de figuur vind
je een dendogram (boomstructuur). Als je in het dendogram
met je muis over de bolletjes bij de splitsingen gaat zie je punten oplichten die onder de betreffende splitsing vallen.
Hoeveel stappen zijn er gemaakt om tot het resultaat te komen? Ben je tevreden over het resultaat? - Kies weer de hiërarchische methode "Single linkage" en kies de dataset "Three equal circles". Druk op de het zwarte knopje en heb veel geduld. Hoeveel stappen zijn er gemaakt om tot het resultaat te komen? Ben je tevreden over het resultaat?
- Wat leer je uit de bovenstaande opdrachten?
- Verdiepende opdracht: In de vorige opdracht heb je met een klein experiment twee methoden vergeleken. Ga naar de site towards data science. Daar staat informatie over verschillende clustermethoden waaronder $K$-means clustering en Agglomerative Hierarchical Clustering (= Single linkage). Zoek in de tekst de voordelen en de problemen bij deze twee methoden. Ook op de site Analytixslab worden voor en nadelen van deze methoden beschouwd (Agglomerative Hierarchical Clustering heet hier AGNES). Wordt hier de zelfde informatie gegeven?
- Verdiepende opdracht: Ga weer naar de site educlust. Maak je eigen keuze van methoden die je wilt vergelijken. Zoek vervolgens uit hoe de methoden precies werken en wat de voor en nadelen van de methoden zijn. Verwerk je onderzoek in een verslag (website / tekstdocument / poster)