Inleiding

Dit hoofdstuk bevat algemene informatie over neurale netwerken en is ook de inleiding bij de verdieping neurale netwerken.

In het hoofdstuk machine learning hebben we drie categorieën leerstrategiën besproken, supervised, unsupervised en reinforcement learning. Zo leert een systeem voor het vinden van passende reclame met unsupervised learning: de associatie-analyse. Artificiële of kunstmatige neurale netwerken (ANN) leren vooral via supervised learning en reinforcement learning. De reden hiervoor is dat neurale netwerken worden ingezet als de relatie tussen de gegevens en de bij een gegeven horende uitkomst, die door de AI-applicatie moet worden voorspeld, ingewikkeld of zelfs niet bekend is. Aan de hand van input-output voorbeelden moet het netwerk leren wat de relatie is. Denk aan Quickdraw: wanneer iemand een slordige schets maakt, is niet bekend wat het voorstelt. Je moet ernaar raden. Neurale netwerken moeten getraind worden. Je geeft Quickdraw een tekening en zegt wat het is. Daardoor leert het systeem (supervised learning). Training kan doorgaan als het systeem eenmaal in bedrijf is: Je geeft QuickDraw een tekening. QuickDraw zegt wat (het denkt dat) het is en je zegt of dat goed of fout is. Ook daarvan leert het systeem (reinforcement learning).

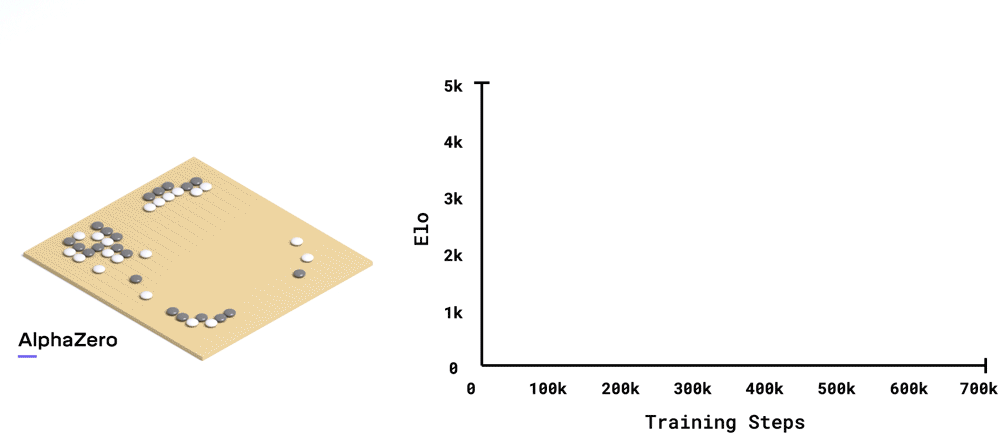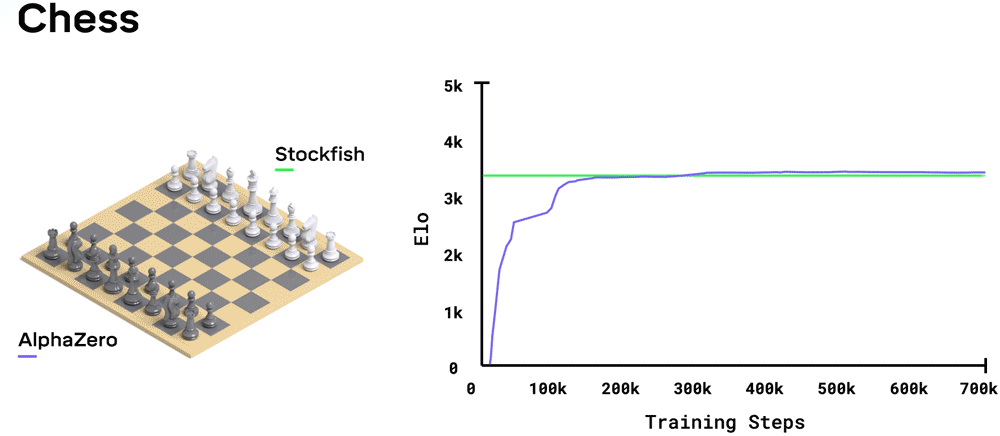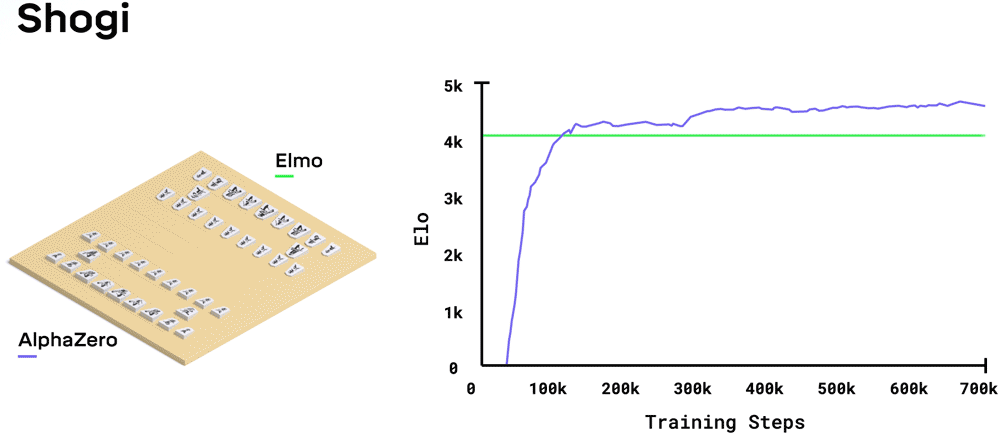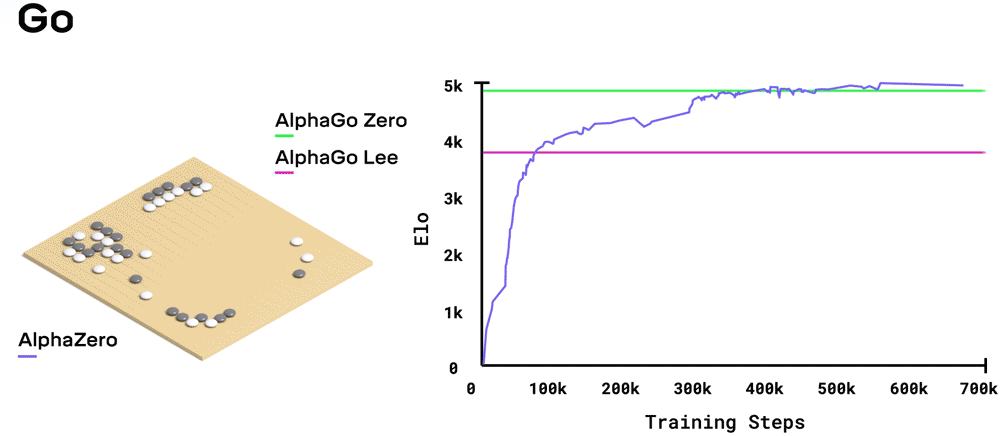
AlphaZero (zie afbeelding) is een AI applicatie van het onderzoeksbedrijf DeepMind dat de bordspelen go, shogi en schaken onverslaanbaar kan leren. Bij al deze spellen zijn de regels van het spel precies bekend, alleen zijn het aantal mogelijke patronen zo enorm groot dat de snelste computer niet alle zetten door kan rekenen. Om toch onverslaanbaar te worden is het netwerk getraind door de computer miljoenen keren tegen zichzelf te laten spelen (reinforcement learning).

Figuur 1: Bij schaken deed AlphaZero het al na vier uur beter dan Stockfish; bij shogi deed AlphaZero het na twee uur beter dan Elmo; en bij go had AlphaZero 30 uur nodig om beter te worden dan zijn voorganger AlphaGo die de legendarische speler Lee Sedol in 2016 versloeg. N.B.: elke trainingstap representeert 4,096 bord posities. Bron: DeepMind

Toepassingen

Hieronder zijn enkele standaardtoepassingen van neurale netwerken weergegeven die aanwezig zijn in verschillende computer programma's . Dit is geenszins een uitgebreide lijst van toepassingen van neurale netwerken, maar hopelijk geeft het je een algemeen beeld van de functies en mogelijkheden.

• Patroonherkenning - We hebben dit al verschillende keren genoemd en het is waarschijnlijk de meest voorkomende toepassing. Voorbeelden zijn gezichtsherkenning, optische tekenherkenning, etc.
• Tijdreeksvoorspelling - Neurale netwerken kunnen worden gebruikt om voorspellingen te doen. Zal de voorraad morgen stijgen of dalen? Zal het regenen of zonnig zijn?
• Signaalverwerking — Cochleaire implantaten (een cochleair implantaat is een apparaat dat aan dove kinderen en volwassenen de mogelijkheid biedt weer iets te horen) en gehoorapparaten moeten onnodig geluid wegfilteren en de belangrijke geluiden versterken. Neurale netwerken kunnen worden getraind om een audiosignaal te verwerken en op de juiste manier te filteren.
• Controle - Misschien heb je gelezen over recente vorderingen op het gebied van onderzoek naar zelfrijdende auto's. Neurale netwerken worden vaak gebruikt om de sturing van fysieke voertuigen (of gesimuleerde voertuigen) te beheren.
• Soft sensors - Een soft sensor verwijst naar het proces van het softwarematig analyseren van een verzameling van vele metingen. Een thermometer kan je de temperatuur van de lucht vertellen, maar wat als je ook de luchtvochtigheid, barometrische druk, dauwpunt, luchtkwaliteit, luchtdichtheid enz. zou weten wat kunnen we dan voorspellen? Neurale netwerken kunnen worden gebruikt om de invoergegevens van veel individuele sensoren te verwerken en als geheel te evalueren.
• Anomaliedetectie - Omdat neurale netwerken zo goed zijn in het herkennen van patronen, kunnen ze ook worden getraind om een output te genereren wanneer er iets gebeurt dat niet in het patroon past. Denk aan een neuraal netwerk dat jouw dagelijkse routine gedurende een lange periode bewaakt. Nadat het netwerk de patronen van jouw gedrag heeft geleerd, kan het je waarschuwen wanneer er iets mis is. (De sensoren in de autostoelen in deze Big Data TED-talk )

Cijferherkenning

We schreven eerder dat je een neuraal netwerk gebruikt wanneer de antwoorden op vragen ingewikkeld, onzeker of zelfs onbekend is. Je denkt dan misschien aan complexe wereldproblemen. maar dat geldt ook al voor schijnbaar heel simpele dingen. Neem bijvoorbeeld het herkennen van cijfers. Simpel, maar niet als het om handschrift gaat.

Hiernaast zie je een trinket (een klein python-programma dat kan draaien in een webpagina). Je kunt daar met je muis een cijfer tekenen. In de trinket zit een neuraal netwerk dat probeert het cijfer te herkennen. Je start de herkenning door op de spatiebalk te drukken. Dit neurale netwerk is al eerder getraind.

Deze applet heeft vergelijkbare fuctionaliteit als Quickdraw, namelijk patroonherkenning.

Misschien herkende de trinket alle cijfers die je tekende, misschien kwam er ook wel eens een fout antwoord. Hieronder zie je de resultaten van een paar pogingen van de auteur.

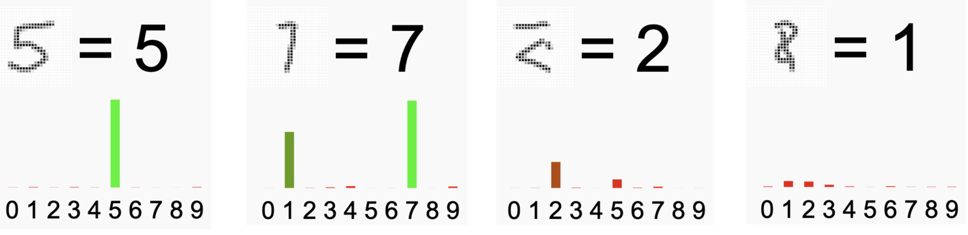
Het meest linkse plaatje is duidelijk, geen twijfel mogelijk. Het plaatje ernaast laat een twijfelgeval zien (1 of 7?), de trinket kiest voor de 7. De andere zijn veel onduidelijker. Het lijkt een handschrift dat voor geen mens te ontcijferen is, laat staan voor een computer.

Wat de trinket duidelijk maakt, is dat het heel anders werkt dan bij de algoritmen en programma's die je eerder maakte. Daar is alles heel precies. Inputs zijn precies omschreven, de stappen in een algoritme zijn dat ook en ten slotte ligt ook precies vast wat een algoritme oplevert. Al kan dat natuurlijk wel een foutmelding zijn.

Hier is alles niet zo duidelijk. De input kan geklieder zijn, de werking is onduidelijk (zometeen meer hierover). De uitkomst is niet zeker, maar heeft een waarschijnlijkheid. Twijfel is mogelijk, een fout antwoord ook.

Een neuraal netwerk kan dus foute antwoorden geven. Om dat te meten zijn twee begrippen belangrijk: recall en precision.

De recall van een mogelijk antwoord $x$ is gedefinieerd als het percentage van de antwoorden $x$ dat correct is. Bij de cijferherkenning is de recall van '1' het percentage van de plaatjes van een 1 die herkend worden als 1. Hier kijk je dus naar het aantal missers.

De precision van een mogelijk antwoord $x$ is gedefinieerd als het percentage van de antwoorden $x$ die ook echt een $x$ zijn. Bij de cijferherkenning: hoeveel van de antwoorden '1' waren ook echt plaatjes van enen (en niet 0, 2, 3, ...). Hier gaat het dus om de fouten.

Ontwerp

Kenmerkend voor een neuraal netwerk is dat het ontwerp gebaseerd is op het menselijk brein. De hersenen zijn eigenlijk een soort netwerk van verbindingen tussen neuronen (zenuwcellen). Neuronen zijn met elkaar verbonden door middel van synapsen (de verbindingen) en geven hierover onderling signalen door. De synapsen bij de dendrieten van een neuron vangen signalen op die door het neuron wordt verwerkt tot een signaal dat de synapsen bij de axonen afgeven. Binnen de kunstmatige neurale netwerken wordt een neuron een perceptron genoemd en is in 1958 door Rosenblatt ontworpen.

Figuur 2: Grafische representatie van een biologische neuron (links) en een kunstmatige neuron ofwel perceptron (rechts)

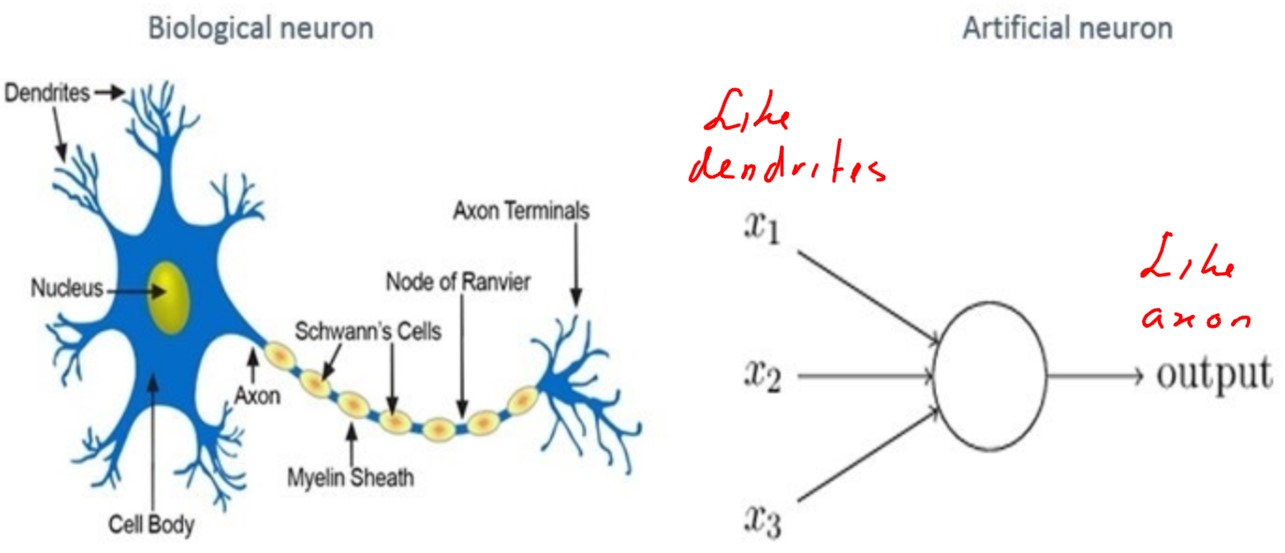
Het doorgeven van signalen heeft een begin een eind. Aan het begin staat een waarneming: je ziet, hoort, voelt, ruikt iets. Aan het eind staat een actie, vaak het aanspannen van spieren. Je ogen zien de bal en je handen vangen die bal. In de hersenen zijn bij het vangen vele neuronen betrokken. Dat je die bal kunt vangen is een vaardigheid die je hebt moeten leren. Bij het creëren van een nieuwe herinnering of het leren van nieuwe vaardigheden worden verbindingen tussen neuronen opgezet en elke keer als je gelijke of vergelijkbare situaties tegen, wordt deze verbinding sterker gemaakt.

Dit is een beknopte en versimpelde uitleg over de werking van het brein, de werkelijkheid is complexer. Daarnaast is ook nog lang niet alles bekend over dit prachtige instrument dat we allemaal bezitten. In deep learning wil men iets vergelijkbaars voor elkaar krijgen met een kunstmatig neuraal netwerk. Een input wordt door een verzameling perceptons (ook knopen genoemd) omgezet in een output:

Figuur 3: De verborgen lagen bevatten perceptrons die samen het neurale netwerk vormen.

Het netwerk moet net als de hersenen voldoende worden getraind om een juiste output te kunnen geven.

Verschillende lagen

Als we meer inzoomen krijgen we het de volgende schematische weergave van een AI applicatie:

Figuur 4: Schematische weergave van een verbonden ANN. De invoer in dit netwerk bestaat uit twee elementen. Er zijn twee verborgen lagen, de eerste met drie knopen en de tweede met twee knopen (perceptrons). Er is in dit voorbeeld slechts één output.

Je ziet in de figuur drie verschillende secties typisch voor de opbouw van een neuraal netwerk:

1. Geef acht

   De input layer (invoerlaag):

   De eerste sectie (links in de figuur) is wat men de input layer noemt. Deze laag kun je beschouwen als de sensoren (b.v. ogen) van het netwerk. De knopen in deze laag (neuronen, perceptrons) vormen de invoer van het netwerk. De knopen uit deze laag krijgen een getalswaarde toebedeeld. Deze waarden kunnen van de gebruiker van de applicatie komen of van de trainer tijdens de training van het netwerk.

   Als het netwerk een tekening moet herkennen, kun je veel inputs hebben die elk de kleurwaarde van een pixel zijn, of het gemiddelde van een groepje pixels.Bij trinket voor de cijferherkenning zijn de inputs de grijswaarden van de pixels. Om het aantal inputs te beperken is de resolutie kleiner gemaakt.

2. De hidden layer (verborgen laag):

   De tweede sectie wordt de hidden layer genoemd en dit de laag is waar ‘the magic happens’. In tegenstelling tot het menselijk brein kunnen geen nieuwe knopen en verbindingen worden aangemaakt in het leerproces. De vorm van de verborgen laag moet voor het trainen door de ontwikkelaar worden bepaald. Wat wel gebeurd is het aanpassen van de sterkte van de verbindingen. Iedere pijl in het schema is een gerichte verbinding tussen knopen. Informatie uit één knoop wordt in de richting van de pijlen doorgegeven aan de volgende knopen. Iedere bij een knoop binnenkomende informatie wordt voorzien van een gewicht. In tegenstelling tot de input layer en de output layer, kunnen er meerdere hidden layers zijn. Wanneer het netwerk complexere taken moet uitvoeren, zoals beeldherkenning, zijn meerdere hidden layers nodig. Het bepalen van de juiste vorm van dit deel van het neurale netwerk is een lastige opgave. Zijn er te weinig knopen of te weinig lagen voor een probleem dan kan het netwerk het niet leren. Maar teveel is ook weer niet goed, het probleem overfitting kan dan makkelijk optreden. Overfitting is het verschijnsel dat er te specifiek voor de trainingsdata wordt geleerd. Een net iets ander datapunt dat wel tot de te leren groep zou moeten horen wordt dan door het netwerk buitengesloten.

3. 

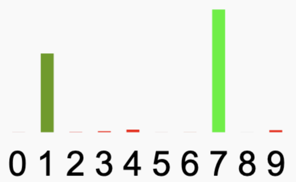
   De output layer (uitvoerlaag):

   Neuronen die zich in de output layer bevinden, zijn bedoeld om de ‘bevindingen’ van het netwerk op te vangen en het terug te geven aan de gebruiker, vandaar de naam ‘output’.

   Bij trinket met de cijferherkenning zijn de outputs de scores van de verschillende cijfers. Hoe hoger de waarde, deste waarschijnlijker dat de schets dat cijfer voorstelt. Hier zijn dus 10 outputs.

Perceptron: input → output

De bouwstenen van het netwerk zijn dus de perceptrons ofwel de neuronen ofwel de knopen.

Figuur 5: De gewichten in de perceptron.

De perceptron in het schema hierboven heeft $n$ verschillende inputs $x_{1},\cdots,x_{n}$. $x_{0}$ is een extra input, de bias, die altijd gelijk aan 1 is. De $n+1$ gewichten $w_{0},\cdots,w_{n}$ moeten worden geleerd. Dit aan de hand van de uitvoer die deze perceptron levert.

De output wordt als volgt berekend. Eerst wordt input van de perceptron wordt met behulp van de gewichten via een gewogen optelling omgezet in een som:

$$ \text{Som}=w_{0}+w_{1}\cdot x_{1}+w_{2}\cdot x_{2}+\cdots+w_{n}\cdot x_{n} $$

Vervolgens wordt deze som aangeboden aan een activeringsfunctie . Deze activeringsfunctie bepaalt de uitvoer. Er worden verschillende activeringsfuncties gebruikt, afhankelijk van het probleem wat met de AI applicatie moet worden opgelost.

Als het netwerk wordt getraind met trainingsdata dan worden de gewichten van alle perceptrons in het netwerk zodanig aangepast dat het netwerk na training de trainingsdata voldoende voorspelt. Wat voldoende is, is afhankelijk van de kwaliteit van de trainingsdata en de gewenste nauwkeurigheid van de voorspellingen door het netwerk. De trainingsdata bestaat uit invoer-uitvoer paren, bij een bepaalde invoer hoort een bepaalde uitvoer (b.v. deze tekening hoort bij een kat, de volgende tekening is een huis, ...). In het algemeen moeten de zelfde trainingsdata herhaaldelijk aan het netwerk worden aangeboden. Na iedere herhaling wordt bepaald of de training voldoende is. Zo niet dan worden in de nieuwe ronde eerste de gewichten op een slimme manier aangepast en wordt opnieuw de uitvoer bepaald. Zo'n reeks herhalingen noemt men, net als bij het trainen bij associatie- en clusteranalyse, recursie.

Hoeveel gewichten moeten er in de training van een neuraal netwerk worden bepaald? We kijken in figuur 6 naar het eerdere voorbeeld. Perceptron h11 ontvangt 2 inputs en bevat dan 3 gewichten evenals de knopen h12 en h2. Knoop h21 ontvangt van de vorige laag 3 inputs en bevat dan 4 gewichten evenals knoop h22. De enige uitvoer perceptron ontvangt 2 inputs en bevat dan 3 gewichten. In totaal $3 \times 3 + 2 \times 4 + 1 \times 3 =20$ gewichten. Je ziet, het aantal te bepalen gewichten is al snel groot.

Figuur 6: perceptron h11 ontvangt 2 inputs en bevat dan 3 gewichten, perceptron h21 ontvangt van de vorige laag 3 inputs en bevat dan 4 gewichten. De uitvoer perceptron ontvangt 2 inputs en bevat dan 3 gewichten. In totaal 3×3 + 2×4 + 1×3 = 20 gewichten.

Ecologische voetafdruk

In vraag 3 hierboven heb je gezien dat er al snel veel parameters geschat moeten worden. Het recursief bepalen van de beste waarden voor parameters is rekenkracht nodig op computers. In de verdieping Neurale netwerken gaan we op het leren van neurale netwerken in en kun je ervaren dat die rekenkracht al merkbaar is bij kleine projecten. Een computer verbruikt energie en hoe meer een computer moet rekenen hoe hoger het energieverbruik wordt. Er zijn een flink aantal artikelen te vinden op het internet die laten zien dat dat verbruik behoorlijk groot kan zijn. Hoe complexer het neurale netwerk hoe groter het aantal parameters en hoe groter het aantal gegevens moet zijn om die parameters te schatten. Hieronder staan twee artikelen, waarvan wij de informatie niet hebben gecontroleerd, die zorgen over het energieverbruik van AI uitspreken.

In het artikel "It takes a lot of energy for machines to learn – here’s why AI is so power-hungry" wordt verteld wat de oorzaken zijn van het enorme verbruik van energie in AI gebruikt in tekstanalyse. Als voorbeeld wordt het model "Bidirectional Encoder Representations from Transformers (BERT)" gegeven. Om Bert te trainen werden 3,3 miljard woorden uit Engelstalige boeken en Wikipedia artikelen. In een training van BERT moet deze verzameling niet één keer maar wel liefst 40 keer worden gelezen. In vergelijking een kind dat leert praten hoort ongeveer 45 miljoen woorden in de eerste 5 levensjaren, 3,000 keer minder dan BERT. BERT één keer trainen kost net zoveel energie als één persoon verbruikt voor een retourvlucht New York - San Fransisco. En voor dat het juiste model is gevonden zijn vele trainingen nodig. Een zeer accurate opvolger van BERT, genaamd GPT-3 heeft een onderliggend neuraal netwerk met maar liefst 175 miljard parameters en verbruikt nog veel meer energie.

Ook het artikel "AI Can Do Great Things—if It Doesn't Burn the Planet" gaat in op het grote energieverbruik van het trainen van AI. Als eerste voorbeeld geven zij het trainen van een robothand om een Rubricscube op te lossen. Volgens de auteurs hebben hiervoor 1000 desktop computers en een flink aantal computers met veel grafische processors voor het rekenwerk maanden gerekend om de training af te ronden. Een ruwe schatting is dat hier 2.8 gigawatt-uren elektriciteit voor is verbruikt, ongeveer gelijk aan de opwekking van elektriciteit gedurende 1 uur door drie kernenergiecentrales.

Omdat steeds meer organisaties AI modellen maken voor toepassingen binnen deze bedrijven is dit energieverbruik een serieus probleem.

Het grotendeels complete overzicht van neurale netwerken

Om een indruk te geven van de complexiteit van de op dit moment bedachte neurale netwerken tonen we je onderstaande figuur. Het verschil in de netwerken zit in de verbindingen tussen de knopen en de wiskundige manier waarop het signaal wordt doorgegeven naar een volgende knoop. In de verdieping concentreren we ons slechts op de typen perceptron (P), feed forward (FF) en deep feed forward (DFF). Meer uitleg over deze figuur vindt je op de website towardsdatascience.com ).