Algoritme: Deze moet je kennen!

Algoritmen die je moet kennen.

Het examenprogramma voor informatica eist dat je een aantal algoritmen moet kunnen reproduceren. In dit hoofdstuk en de volgende worden deze gepresenteerd. Een aantal zijn heel erg simpel, maar jouw taak is om het stap voor stap uit te leggen zodat het direct geprogrammeerd zou kunnen worden. Een aantal van de opdrachten vind je dan ook terug in de cursussen javascript en php programmeren.

Sorteren

In deze paragraaf worden drie sorteeralgoritmen gepresenteerd "bubble sort", "quick sort", "insertion sort". Je kunt ze ook testen samen met de standaard sorteer methode die javascript voor lijsten biedt.

Bubble sort

bron: wikipedia

Bubble sort, soms ook exchange sort of sinking sort genoemd, is een eenvoudig sorteeralgoritme. Het wordt vaak gebruikt als illustratie van een algoritme. Het is een simpel, maar inefficiënt algoritme, vaak gekozen ter illustratie vanwege de eenvoud en omdat het gemakkelijk uit te leggen is.

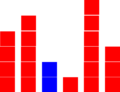
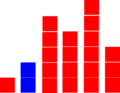
Bubble sort werkt als volgt (flowchart in rechter figuur):

• 1. Loop door de te sorteren rij van n elementen en vergelijk elk element met het volgende. Verwissel beide als ze in de verkeerde volgorde staan. Schuif dan een stapje op.
• 2. Loop opnieuw door de rij, maar ga nu door tot het voorlaatste element, omdat het laatste element het grootste in de rij was.
• 3. Nog een keer, maar negeer dan de twee laatste elementen.
• 4. Ga zo door.
• n. Nog een keer, maar negeer dan de laatste n-1 getallen.
• n+1. Klaar.

We zien (zie linker figuur) de grotere elementen als het ware als luchtbellen naar boven drijven. Aan deze metafoor ontleent het algoritme zijn naam.

Quick sort

bron: wikipedia

Quicksort is een recursief sorteeralgoritme bedacht door Tony Hoare. Hij werkte destijds aan een project in verband met computervertalingen. Daarvoor was het nodig om korte Russische zinnen snel en efficiënt te sorteren. Het algemene werkingsprincipe van quicksort wordt weleens kort omschreven als verdeel en heers.

Werkingsprincipe

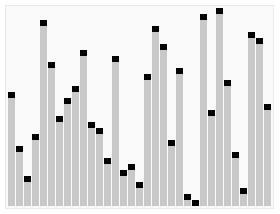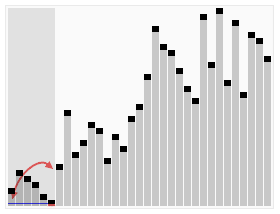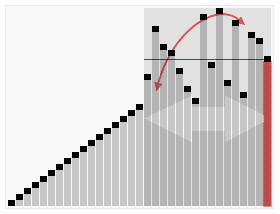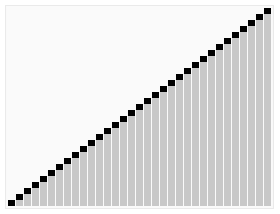
Het doel van quicksort is om een rij van ongesorteerde getallen, gesorteerd terug te geven. Dit gebeurt in 4 stappen.

1. Als de rij één of geen elementen bevat. STOP
2. Kies een willekeurig element in de rij. Dit element, blauw aangeduid in de figuur, wordt de spil of de pivot genoemd.
3. Herschik de rij zodat alle elementen met een waarde kleiner of gelijk aan die van de spil links van de spil belanden en alle elementen met een waarde groter dan die van de spil rechts van de spil belanden. Deze stap wordt het partitioneren genoemd.
4. Sorteer de linker en de rechter deelrij. (Door middel van quicksort.)

Voor partitioneren	Na partitioneren

Hierbij zijn de volgende zaken vermeldenswaardig. In stap 2 wordt een willekeurig element gekozen. Iedere keuze van de spil leidt tot een werkend algoritme. Het willekeurig kiezen van de spil leidt praktisch tot de beste resultaten, al geeft dit enkele theoretische nadelen. Zo is het moeilijk om het algoritme te analyseren. Bovendien voldoet een algoritme dat een willekeurige stap bevat niet aan de striktere definities van een algoritme. In stap 3 wordt niet gespecificeerd hoe deze stap door een computer uitgevoerd moet worden. Er zijn verschillende implementaties waarvan die van Nico Lomuto op wikipedia wordt gepresenteerd. Het exacte verloop van deze stap wordt onder de kop partitionering besproken. In stap 4 roept het algoritme zichzelf op. Quicksort is dus een recursief algoritme.

Insertion sort

bron: wikipedia

Werking

Het begint door de eerste twee elementen uit de set te sorteren. Als deze op hun plaats staan, voegen we het derde element op de juiste plaats toe. Dit doen we totdat we alle elementen op hun plaats hebben gezet.

Dit is eigenlijk de manier waarop een speler zijn kaarten schikt bij een kaartspel. Vandaar dat deze routine ook de Cardsort genoemd wordt.

Test sorteeralgoritmen

Het vergelijken van de snelheid van sorteeralgoritmes is altijd leuk geweest. Het is duizenden malen uitgevoerd, tijd en energie kostend. Maar je moet het ook zelf eens proberen. Behalve dat het leuk is, is het vergelijken van de snelheid van sorteer algoritmen erg nuttig voor toepassingen. Bedrijven en organisaties moeten heel vaak data sorteren. Het is dus nuttig de beste methode te vinden. De code voor deze test is te vinden in sorteer.js. De graphics en de tabel worden door code in deze bladzijde verzorgd. Het begrijpen van deze code vergroot zeker jouw kennis van programmeren.
Probeer deze bladzijde ook eens uit in verschillende browsers op dezelfde computer. Er zijn grote verschillen.

Een c++ test van de sorteermethoden op een linux machine door Vinayak Garg.

Simulatie van de sorteeralgoritmen
Geef aantal elementen.
Geef aantal simulaties
Voer uit

Vragen

1. Quick sort, bubble sort en insertion sort hebben in het slechtste geval, dat wil zeggen de minst gunstige begin volgorde, evenveel stappen nodig om deze te sorteren.
   Dit aantal is gelijk aan $(n-1) + (n-2) + \dots + 2 + 1 = \frac{1}{2}(n-1)n$
   1. Toon dit aan in het geval dat er 7 elementen in de lijst zitten.
   2. Toon dit aan in het geval dat er 8 elementen in de lijst zitten.
   3. Beargumenteer nu ook het algemene geval voor $n$ elementen in de lijst.
2. Zoals in de figuur is te zien is de neemt gemiddelde tijd voor het sorteren niet op dezelfde manier toe bij een toename van het aantal elementen. De manier waarop het aantal berekeningen of de tijd toeneemt bij toenemende $n$ noemt men de orde $O$ van een methode. De orde van bubble en insertion sort is $O(n^{2})$ ofwel de tijd neemt evenredig toe met $n^{2}$. Dus $T_{bubble}(n) = a n(n-1) $ en $T_{insertion}(n) = b n^{2} $. Quick sort is orde $O(n log(n))$ dus $T_{quick}(n) = c n \log(n)$.
   1. Voer met de tool in deze bladzijde 50 simulaties uit voor respectievelijk 1000, 5000, 10000 en 20000 elementen. Verzamel de tijden in b.v. Excel
   2. Bereken $a$, $b$ en $c$ met de uitkomsten voor 20000 elementen.
   3. Voorspel met deze $a$, $b$ en $c$ de tijd nodig voor 1000, 5000 en 10000 elementen. Is dit ongeveer in overeenstemming met de gevonden resultaten? Zie hier voor een uitwerking
   4. Leg uit waarom op een ander type computer of in een andere browser of zelfs in een herhaling van de simulatie waarschijnlijk andere waarden voor $a$, $b$ en $c$ worden gevonden. Antwoord Er zijn voor 20000 elementen $20000! = 20000 \times 19999 \times \dots \times 2 \times 1$ verschillende volgorden te maken met 20000 elementen, heel veel dus. Wij simuleren er daar slechst 50 van, een heel klein deel dus. Daarnaast is de ene computer sneller dan de ander en heeft de ene browser op een andere manier javascript geïmplementeerd dan een andere browser.