Zelf aan de slag met wiskundige technieken in AI

John Val/ Informatica/ Informatie/ Kunstmatige Intelligentie /associatie analyse

Editor: John Val

Inleiding Associatieanalyse Clusteranalyse

Aanvullende theorie: (150 minuten) bron:Lesmodule Big Data

Artificiële Intelligentie en data analyse

Toepassingen in Big Data kunnen, zoals we al hebben gezien het hoofdstuk Trends in deze AI cursus en de hoofdstukken Big Data en De kosten van Gratis uit de overkoepelende cursus Informatie, nuttig zijn maar ook een bedreiging vormen voor het individu. Maar hoe wordt de informatie geleverd door dit soort toepassingen verkregen uit de data?

De meeste van deze toepassingen gebruiken Artificiële Intelligentie om b.v. patronen te herkennen of groeperingen te maken, technieken die we zijn tegen gekomen in het hoofdstuk Technieken. In dit deel van de cursus gaan we een paar van die wiskundige technieken verder uitwerken. Ben jij een leerling die geïnteresseerd is in wiskunde en de toepassingen van wiskunde voel je dan uitgedaagd. De berekeningen in dit hoofdstuk zijn echter niet ingewikkeld en zijn voor iedere leerling op havo en vwo makkelijk uit te voeren.

Associatieanalyse met behulp van verzamelingenleer

Bij associatieanalyse is het de bedoeling dat we een gegeven set kenmerken (bijvoorbeeld jouw leeftijd, geslacht, ingetypte zoekopdracht, beluisterde muziek) kunnen koppelen aan een andere set kenmerken (bijvoorbeeld reclame passend bij doelgroep omschrijving, leeftijd en geslacht ). Het resultaat van de associatie is dan de uitvoer van de toepassing (bijvoorbeeld de reclame die in de zoekmachine verschijnt, muziek die jij ook wel leuk zou vinden).

De wiskundige techniek gebruikt in associatieanalyse is de verzamelingenleer. Laten we eens kijken wat de verzamelingenleer inhoud.

Symbolen
Notatie Betekenis
$\in$ ’is een element van’, ’behoort tot’
$\subset$ ’is een deelverzameling van’
{,} accolades worden gebruikt om een verzameling aan te duiden
$\cap$ ’doorsnede’, het gemeenschappelijke deel van de twee verzamelingen
$\cup$ ’vereniging’, de elementen van de eerste en tweede verzameling worden samengenomen
$\#$ ’aantal’, $\# A$ is het aantal elementen in $A$.
$\Rightarrow$ ’implicatie’, al links waar is dan is ook rechts waar.

Verzamelingenleer

In plaats van een ‘groep’ spreken we van een verzameling ($V$) (set). In een verzameling bevindt zich individuen, beter bekent als elementen $$V=\{v_{1},v_{2},v_{3},\cdots ,v_{n}\}.$$
Een verzameling representeert een aantal elementen met een bepaalde gezamenlijke eigenschap ($x$), zoals de eigenschap ‘mens’ of ‘plezierig’. Een verzameling bestaat uit elementen, en als $x$ een element van een verzameling $X$ noteren we dit als $x \in X$. We gebruiken accolades { en } om verzamelingen te noteren. We gebruiken binnen de accolades het symbool | om elementen met bepaalde eigenschappen aan te geven, zoals in $\{x \in \mathbb{N} | x \, is\, deelbaar \, door \, 2 \}$
Zo is bijvoorbeeld $\{Melk , Brood , Kaas\}$ de verzameling met de elementen melk, brood, en kaas en $Melk \in \{Melk , Brood , Kaas\}$, melk is een element van deze verzameling.

Relaties tussen verzamelingen
$X \subset Y$
Y X

Als voor twee verzamelingen $X$ en $Y$ geldt dat elk element van $X$ ook een element is van $Y$, dan zeggen we dat $X$ een deelverzameling (subset) is van $Y$. Notatie: $X \subset Y = \{ \forall x: x \in X \rightarrow x \in Y \} $

Zo is bijvoorbeeld $X=\{Melk , Kaas\}$ een deelverzameling van $Y = \{Melk , Brood , Kaas\}$

$X \cap Y$
X⋂Y Y X

De doorsnede (intersection) $X \cap Y$ van twee verzamelingen $X$ en $Y$ bestaat uit de gemeenschappelijke elementen van $X$ en $Y$. $X \cap Y = \{ x| x \in X \, \wedge \, x \in Y \}$

Zo is bijvoorbeeld $\{Melk , Brood , Kaas\} \cap \{Melk , Brood , Pindakaas\}$ de verzameling met de elementen $Melk$ en $Brood$.
$\{Melk , Brood , Kaas\} \cap \{Melk , Brood , Pindakaas\} = \{Melk , Brood\}$

$X \cup Y$
X⋃Y Y X

De vereniging (union) $X \cup Y$ van twee verzamelingen $X$ en $Y$ bestaat uit de elementen die tot $X$, tot $Y$ of tot beide horen. $X \cup Y = \{ x| x \in X \, \vee \, x \in Y \}$.

Zo is bijvoorbeeld $\{Melk , Brood , Kaas\}\cup\{Melk , Brood , Pindakaas\}$ de verzameling met de elementen $Kaas, Melk, Brood$ en $Pindakaas$. $\{Melk , Brood , Kaas\}\cup\{Melk , Brood , Pindakaas\} = \{Kaas, Melk, Brood, Pindakaas\}$

Voor eindige verzamelingen $A$ definieren we $\#(A)$ als het aantal elementen in $A$. Zo is bijvoorbeeld $\#({Chips,Zeep,Appels})=3$.

Een element van een verzameling kan zelf ook een verzameling zijn. Zo bestaat de verzameling $C= \{ \{ Chips,Zeep,Appels \}, \{Chips,Zeep,Appels\}, \{Zeep,Bananen\},\{Chips,Zeep,Bananen\}\}$ uit vier elementen.

Binnen de verzamelingenleer definiëert men een dergelijke verzameling waarvan de elementen ook weer verzamelingen zijn als een collectie.
Nog voorbeeld is de collectie: $$D=\{\{banaan\},\{chips\},\{melk\},\{pruim\},\{banaan,rum\},\{chips,rum\},\{banaan,chips,melk\}, \{banaan,rum,melk,pruim\}\}$$ De collectie $D$ bestaat dus uit de verzamelingen:
$T1=\{banaan\}$,
$T2=\{chips\}$,
$T3=\{melk\}$,
$T4=\{pruim\}$,
$T5=\{banaan,rum\}$,
$T6=\{chips,rum\}$,
$T7=\{banaan,chips,melk\}$ en
$T8=\{banaan,rum,melk,pruim\}$

Associatieregels

Om uitspraken te kunnen doen over verbanden tussen verzamelingen en de waarde van die verzamelingen zijn de volgende definities van belang:

Voor de bovenstaande collectie $D$ geldt:

Een praktische toepassing: Bij marktonderzoek is de support van een stel artikelen (b.v. $K=\{televisie,surround set\}$) het aantal klanten dat al die artikelen koopt, meestal als percentage van het totaal aantal klanten.

Een stel artikelen $K$ met hoge support (boven een zekere drempel) heet frequent (Ofwel ten opzichte van het totaal aantal klanten kopen veel klanten alle artiklen in $K$).

Een itemset is een deelverzameling van elementen van een stel artikelen. Een $k$-itemset is een deelverzameling die $k$ elementen bevatten.

Er moet voldoende vertrouwen zijn in de associatieregel. Om dit te kunnen bepalen, berekent men de confidence van de associatieregel.

De confidence van $X \Rightarrow Y$ is per definitie de support van de vereniging van $X$ en $Y$ gedeeld door de support van $X$.
In notatievorm: $confidence(X \Rightarrow Y) = \frac{support(X \cup Y)}{support(X)}$
Omdat $\frac{support(X \cup Y)}{support(X)}=\frac{frq(X \cup Y)}{frq(X)}$, geldt ook: $confidence(X \Rightarrow Y) =\frac{frq(X \cup Y)}{frq(X)}$

Bij marktonderzoek is de confidence een maat voor de kans dat iemand $Y$ koopt, gegeven dat hij $X$ ook in zijn boodschappenmandje heeft.

Associatieregel: $\{banaan\} \Rightarrow \{𝑟𝑢𝑚\}$ in $D$ (zie boven):
$confidence(\{ banaan\} \Rightarrow \{ rum \} )= \frac{support(\{ banaan,rum\})}{support(\{banaan\})}=\frac{\frac{2}{8}}{\frac{4}{8}}=\frac{1}{2}$ (=50%)
Want: $support(\{ banaan,rum\})= \frac{2}{8}$ en $support(\{banaan\})= \frac{4}{8}$

Apriori algoritme

Er bestaan veel algoritmes om associatieregels te ontdekken. De oudste en meest bekende methode is het Apriori principe (a priori : op basis van eerder onderzoek) ontwikkeld voor transacties (verkopen). Het is in de jaren negentig bedacht door Agrawal en anderen. Gegeven een drempelwaarde $C$ identificeert het algoritme alle itemsets (deelverzamelingen) in de gehele dataset die minstens $C$ transacties in de database bevatten.
Apriori gebruikt een "bottom up" aanpak. Veel voorkomende subsets worden item voor item uitgebreidt (een stap genoemd kandidaat generatie ), waarna de groepen van kandidaten worden getoetst tegen de gehele dataset. Het algoritme stopt als er geen succesvolle uitbreiding gevonden kan worden. Het is gebaseerd op de volgende observatie. Iedere deelverzameling van een frequente itemset (veel voorkomende itemset) is zelf ook weer een frequente itemset.

Het Apriori algoritme bestaat uit twee fasen:
  1. Het genereren van verzamelingen of itemsets die mogelijk aan de drempelwaarde voldoen (ofwel de minimale support hebben). Dit worden kandidaten genoemd.
  2. Het selecteren van de kandidaten die werkelijk aan de drempelwaarde voldoen (de minimale support hebben).

Deze fasen worden per niveau uitgevoerd, dus voor verzamelingen of items met grootte 1, met grootte 2, enzovoort.
Het algoritme stopt wanneer er geen kandidaten meer gevonden kunnen worden.

Methode

De flowchart hiernaast geeft de grafische weergave van het algoritme. Hieronder behandelen we de stappen aan de hand van een voorbeeld.

Collectie $W$
Id Items
0 $\{Spaghetti, Tomatensaus\}$
1 $\{Spaghetti, Brood\}$
2 $\{Spaghetti, Tomatensaus, Brood \}$
3 $\{Brood,Boter\}$
4 $\{Brood, Tomatensaus\}$

Stel je hebt als winkel een groot aantal verkopen per klant, (Collectie $W$) Vraag: Genereer de grootste k-itemsets met behulp van het Apriori-algoritme. Zorg voor een minimale support van 40%.
Iteratie met k=1

  1. Genereer alle deelverzamelingen (itemsets) kandidaten met lengte $1$.
    $C_{1}=\{\{Spaghetti\}, \{Tomatensaus\},\{ Brood \}, \{Boter \}\}$
  2. Bereken support van de kandidaat deelverzamelingen (1-itemsets) uit $C_{1}$ in $W$.
    Itemset Support
    $\{Spaghetti\}$ 60%
    $\{Tomatensaus\}$ 60%
    $\{Brood \}$ 80%
    $\{Boter\}$ 20%
  3. De support van kandidaat itemset $\{Boter\}$ is onder de 40% en voldoet dus niet.
    De frequente 1-itemsets zijn dus: $F_{1}=\{\{Spaghetti\}, \{Tomatensaus\}, \{Brood\}\}$
  4. $F_{1}$ is niet leeg. We gaan op zoek naar grotere frequente itemsets namelijk die uit twee elementen bestaan. k=2

Iteratie met k=2

  1. Genereer alle deelverzamelingen (itemsets) kandidaten met lengte $2$ met elementen uit $F_{1}$.
    $C_{2}=\{\{Spaghetti,Tomatensaus\}, \{Spaghetti, Brood \}, \{Tomatensaus, Brood \}\}$
  2. Bereken support van de kandidaat deelverzamelingen (2-itemsets) uit $C_{2}$ in $W$.
    Itemset Support
    $\{Spaghetti, Tomatensaus \}$ 40%
    $\{Spaghetti, Brood \}$ 40%
    $\{Tomatensaus, Brood \}$ 40%
  3. Alle voldoen aan de 40% eis dus zijn de frequente 2-itemsets:$F_{2}=\{\{Spaghetti,Tomatensaus\}, \{Spaghetti, Brood \}, \{Tomatensaus, Brood \}\}$
  4. $F_{2}$ is niet leeg. We gaan op zoek naar grotere frequente itemsets namelijk die uit drie elementen bestaan. k=3

Iteratie met k=3

  1. Genereer alle deelverzamelingen (itemsets) kandidaten met lengte $2$ met elementen uit $F_{2}$.
    $C_{3}=\{\{Spaghetti,Tomatensaus, Brood \}\}$
  2. Bereken support van de kandidaat deelverzamelingen (3-itemsets) uit $C_{3}$ in $W$.
    Itemset Support
    $\{Spaghetti,Tomatensaus, Brood\}$ 20%
  3. De support van 3-itemset $\{Spaghetti,Tomatensaus, Brood\}$ voldoet niet dus is :$F_{3}=\{\}$
  4. $F_{3}$ is leeg. We zijn bij het einde gekomen.

Na het einde bestaat de uiteindelijke set van voldoende frequente verzamelingen uit
$F=\{\{Spaghetti\}, \{Tomatensaus\}, \{Brood\}, \{Spaghetti,Tomatensaus\}, \{Spaghetti, Brood \}, \{Tomatensaus, Brood \}\}$.
Hieruit kunnen we onderstaande associatie regels afleiden. De eerste regel zegt bijvoorbeeld dat in 67% van de gevallen dat een klant spaghetti koopt, koopt deze ook brood.

Associatieregels Confidence
$\{Spaghetti\} \Rightarrow \{Spaghetti,Tomatensaus\}$ $\frac{40}{60}= 67 \% $
$\{Spaghetti\} \Rightarrow \{Spaghetti,Brood\}$ $\frac{40}{60}= 67\% $
$\{Brood\} \Rightarrow \{Spaghetti,Brood\}$ $\frac{40}{60}= 67\% $
$\{Brood\} \Rightarrow \{Spaghetti,Brood\}$ $\frac{40}{80}= 50\% $
$\{Brood\} \Rightarrow \{Tomatensaus,Brood\}$ $\frac{40}{80}= 50\% $
$\{Tomatensaus\} \Rightarrow \{Tomatensaus,Brood\}$ $\frac{40}{60}= 67\% $
$\{Spaghetti\} \Rightarrow \{Tomatensaus,Spaghetti\}$ $\frac{40}{60}= 67\% $

Clusteranalyse


Figuur 5.3.1 Het classificeren van objecten

Figuur 5.3.2 De stelling van Pythagoras

Inleiding

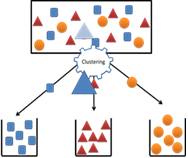
Clusteranalyse is het classificeren of het groeperen in 'clusters' of 'klassen' van objecten op grond van hun kenmerken. Het doel van clusteranalyse is het vormen van deelverzamelingen die elk hun eigen gedeelde kenmerken bevatten.
Het doel van clusteranalyse is het verdelen van een dataset in groepen. Deze groepen en het aantal groepen zijn vooraf niet bekend. Het streven is zoveel mogelijk gelijkenis binnen een groep en zoveel mogelijk verschil tussen de groepen te krijgen. In tegenstelling tot classificatie: daar weten we de indeling in groepen al, en willen we een nieuw object in de juiste groep krijgen. Clusteranalyse is vooral bekend uit marktonderzoek en wordt veel ingezet om het koopgedrag van klanten te onderzoeken. Het doel van de analyse is niet het voorspellen van dit koopgedrag, maar het zoeken naar een beperkt aantal groepen klanten met hetzelfde koopgedrag. Online kan deze techniek heel goed worden ingezet om websitebezoek te onderzoeken. Hiermee kunnen verschillende doelgroepen op een effectieve wijze benaderd worden. Een bedrijf krijgt zo zicht op welk product of dienst een groep klanten het beste aansluit, en welke product eventueel niet haalbaar of minder bereikbaar zijn voor de klantengroep.
In de biologie zijn er meerdere gebieden waar clusteranalyse wordt toegepast. Denk bijvoorbeeld aan de classificatie van verschillende organismen. Elk organisme hoort bij een soort. Soorten kunnen op hun beurt weer worden onderverdeeld in lagere taxa, zoals ondersoort en variëteit. Soorten zelf worden samengevoegd in geslachten en deze weer in families en in taxa van nog hogere rang. Een ander voorbeeld van het gebruiken clustertechnieken in de biologie is het maken van groepen met genen die zie een bepaalde erfelijke ziekte kunnen bevatten. Door het gebruik van clustermethodes kunnen de groepen met genen gevonden worden. Als deze groepen bekend zijn, wordt het gemakkelijk een medicijn te ontwikkelen dat de erfelijke ziekte kan voorkomen of genezen.

Afstandsmaten

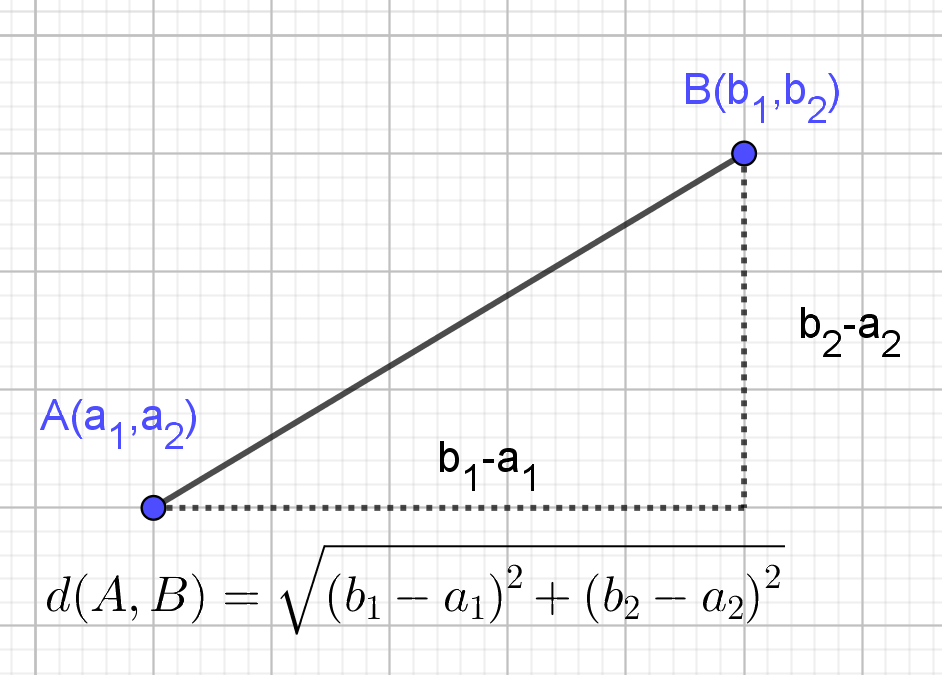
Afstand tussen twee punten In de wiskunde kan de afstand worden berekend als de wortel uit de som van de kwadraten van de verschillen tussen de coördinaten, volgens de stelling van Pythagoras, zie Figuur 3.5.2. Deze afstand noemen we de Euclidische astand. In drie dimensies en hoger wordt deze op een zelfde manier berekend.

Afstand tussen datapunten (objecten):

Dit is een maat die aangeeft hoe groot de ‘overeenkomst’ of het ‘verschil’ is tussen twee kenmerk datapunten.
Er zijn twee bekende methoden om de afstand tussen waarnemingen:

De definitie van de Euclidische afstand tussen twee punten $A=(a_{1},a_{2},\dots , a_{n-1}, a_{n})$ en $B=(b_{1},b_{2},\dots , b_{n-1}, b_{n})$ is:
$$\begin{array}{rcl}d(A,B)& = &\sqrt{\sum_{i=1}^{n}(a_{i}-b_{i})^{2} }\\ & = &\sqrt{(a_{1}-b_{1})^{2}+ (a_{2}-b_{2})^{2}+ \dots + (a_{n}-b_{n})^{2}}\end{array}$$
De definitie van de Manhattan of City-block afstand tussen twee punten $A=(a_{1},a_{2},\dots , a_{n-1}, a_{n})$ en $B=(b_{1},b_{2},\dots , b_{n-1}, b_{n})$ is:
$$\begin{array}{rcl}d(A,B)& = &\sum_{i=1}^{n} |a_{i}-b_{i}|\\ & = &|a_{1}-b_{1}|+ |a_{2}-b_{2}|+ \dots + |a_{n}-b_{n}|\end{array}$$
Voorbeeld A
Geef de afstand tussen de volgende objecten in een 5 dimensionale ruimte:
Object $A$ 10 12 15 13 9
Object $B$ 18 23 13 15 17

De Manhattan of City-block afstand is: $d(A,B)= |10−8|+|12−23|+|15−13|+|13−15|+|9−17|=25$

De Euclidische afstand is: $d(A,B)=\sqrt{(10−18)^{2}+(12−23)^{2}+(15−13)^{2}+(13−15)^{2}+(9−17)^{2}} =16,16$

Afstandsmatrix

Een matrix van afstanden is een matrix waarvan de elementen de afstanden tussen de punten aangeven.

Twee dimensionale Euclidische afstand $d(A,B)=\sqrt{(a_{1}-b_{1})^{2}+ (a_{2}-b_{2})^{2}}$

Voorbeeld B

Gegeven een dataset met vier objecten.
Geef de afstandsmatrix.
xy
A21
B42
C61
D72
Gebruiken we de gewone Euclidische afstand dan
ziet de afstandsmatrix er als volgt uit:
ABCD
A02.2445.1
B2.2402.243
C42.2401.41
D5.131.410

Afstand tussen clusters

Als je de afstand tussen elk paar van objecten weet, wat is dan de afstand tussen twee clusters $C_{1}$ en $C_{2}$?
We nemen hier de kleinste afstand tussen twee objecten waarvan er één in $C_{1}$ aanwezig is en de andere in $C_{2}$. Deze afstand noemt men Single Linkage.

Single Linkage: $d(C_{1},C_{2})=\min\{d(A,B)|A \in C_{1}\,\,en\,\, B \in C_{2} \}$

Voorbeeld C

Gegeven een dataset met zes punten.
xy
$A_{1}$13
$A_{2}$14
$A_{3}$22
$B_{1}$51
$B_{2}$52
$B_{3}$72
De clusters zijn $C_{1}=\{A_{1},A_{2},A_{3}\}$ en $C_{2}=\{B_{1},B_{2},B_{3}\}$
Geef de minimale afstand tussen $C_{1}$ en $C_{2}$
De afstandsmatrix is:
$B_{1}$$B_{2}$$B_{3}$
$A_{1}$4.474.126.03
$A_{2}$54.476.32
$A_{3}$3.1635
$d(C_{1},C_{2})=\min\{d(A,B)|A \in C_{1}\,\,en\,\, B \in C_{2} \}$
$d(A_{3},B_{2})=\sqrt{(5-2)^{2}+(2-2)^2}=3$ is de kleinste afstand en is dus de afstand tussen $C_{1}$ en $C_{2}$.

Centrum cluster

Het centrum $M(m_{1},m_{2}, \dots, m_{n})$ van een cluster wordt bepaald als het gemiddelde van de coördinaten van de punten in de cluster. Wiskundig gezien is het het zwaartepunt van de veelhoek die door de punten wordt gevormd.

Centrum $M$ van een cluster:
$M(m_{1},m_{2}, \dots, m_{n})= \left( \frac{\sum^{1}_{n} a_{1i}}{n},\frac{\sum^{1}_{n} a_{2i}}{n}, \dots, \frac{\sum^{1}_{n} a_{ni}}{n}\right)$.

Voorbeeld D

Gegeven een cluster $C$ die de volgende objecten bevat:
xy
$A_{1}$00
$A_{2}$78
$A_{3}$48
$A_{4}$30
Bereken het centrum van de cluster $C$.
$C=\{A_{1},A_{2},A_{3},A_{4}\}$
$M= \left( \frac{0 + 7 + 4 +3 }{4},\frac{0+8+8+0}{4}\right)=( 3\frac{1 }{2},4)$

Clustermethoden

Er zijn twee methodes om tot clusters te komen: hiërarchische of partitiemethode. In deze paragraaf gaan we ons beperken tot niet-hiërarchisch clustering.
Niet-hiërarchisch of partitioneren betekent het stap voor stap verbeteren van een bestaande clustering.

$K$-means-clustering

Het oudste en meest bekende clusteralgoritme is de $K$-means methode. Later zijn er veel varianten ontwikkeld die gebaseerd zijn op deze methode. $K$-means is een eenvoudige, iteratieve manier van clusteren. Vooraf wordt bepaald hoeveel clusters je wilt hebben. Om de optimale verbetering van een bestaande clustering te vinden ga je als volgt te werk:

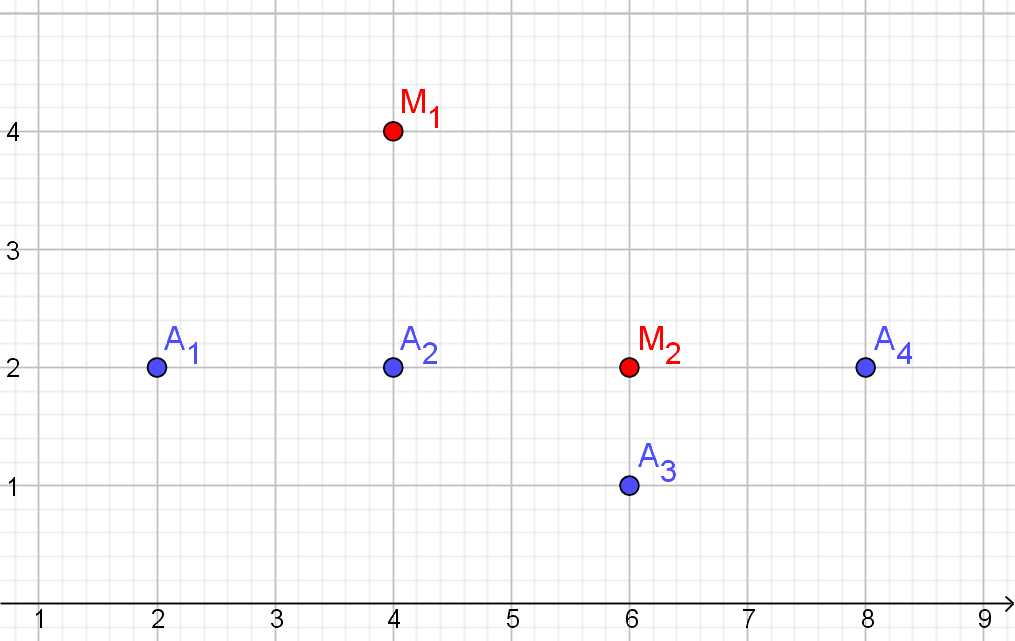
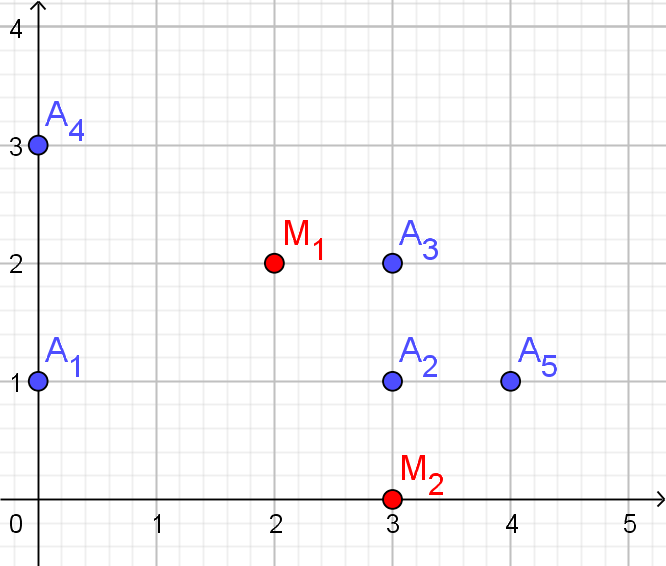
Start: Kies de centra van de clusters eerste keer gewoon willekeurig.
  1. Daarna bepaal je van elk datapunt de afstand tot ieder centrum, en wijs het datapunt toe aan de cluster waarvan het centrum het dichtstbij is.
  2. Als de clusters veranderen en men nog niet voorbij het vooraf gekozen aantal stappen is ga dan naar stap 3. Anders zijn we klaar.
  3. Nadat alle datapunten aan een cluster zijn toegevoegd, bereken je de centra van iedere cluster opnieuw. Hiervoor gebruik je voor ieder cluster apart de volgende formule:
    $M(m_{1},m_{2}, \dots, m_{n})= \left( \frac{\sum^{1}_{n} a_{1i}}{n},\frac{\sum^{1}_{n} a_{2i}}{n}, \dots, \frac{\sum^{1}_{n} a_{ni}}{n}\right)$.
    $n$ is dan het aantal elementen in één cluster.
    Ga naar stap 1.

Voorbeeld E

Gegeven een cluster $C$ die de volgende objecten bevat:
xy
$A_{1}$22
$A_{2}$42
$A_{3}$61
$A_{4}$82
We bepalen vooraf dat we twee clusters willen, dus $k=2$.
Geef de uitwerking van de eerste twee iteraties.
Als afstandsmaat gebruik je de normale (Euclidische) afstand.
Start:
Kies twee willekeurig centra. $M_{1}=(4,4)$ en $M_{2}=(6,2)$
Iteratie 1:
  1. De afstandsmatrix wordt:
    $M_{1}$$M_{2}$toewijzing
    $A_{1}$2.834$C_{1}$
    $A_{2}$22$C_{1}$
    $A_{3}$3.611$C_{2}$
    $A_{4}$4.472$C_{2}$
  2. De nieuwe clusters zijn:
    $C_{1}$$\{A_{1},A_{2}\}$
    $C_{2}$$\{A_{3},A_{4}\}$
  3. De nieuwe centra zijn: $M_{1}'=(\frac{4+2}{2},\frac{2+2}{2})=(3,2)$ en $M_{2}'=(\frac{6+8}{2},\frac{1+2}{2})=(7,1.5)$
Iteratie 2:
  1. De afstandsmatrix wordt:
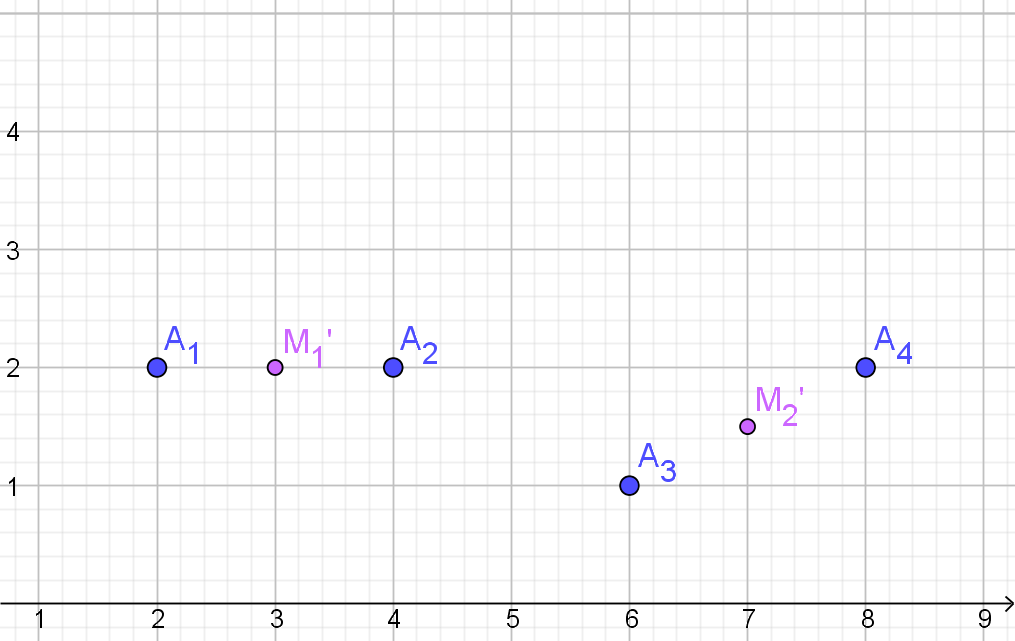
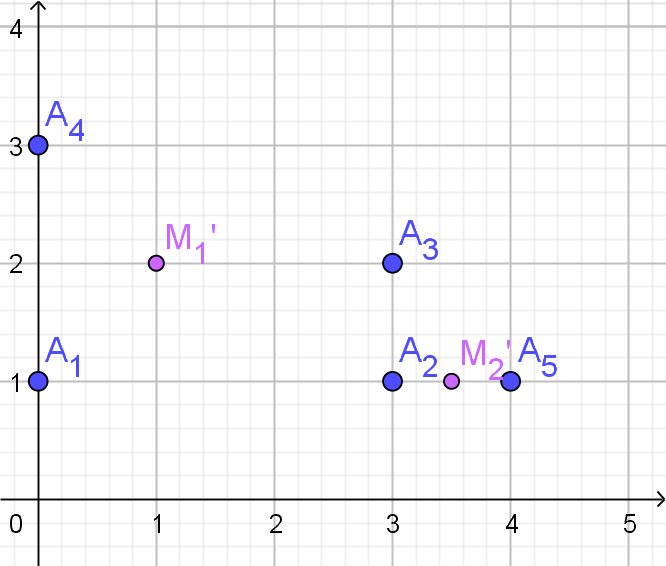
    $M_{1}'$$M_{2}'$toewijzing
    $A_{1}$15.02$C_{1}$
    $A_{2}$13.04$C_{1}$
    $A_{3}$3.161.12$C_{2}$
    $A_{4}$4.471.12$C_{2}$
  2. Er zijn geen nieuwe clusters, dus ook geen nieuwe centra. Stop
Start

Iteratie 1

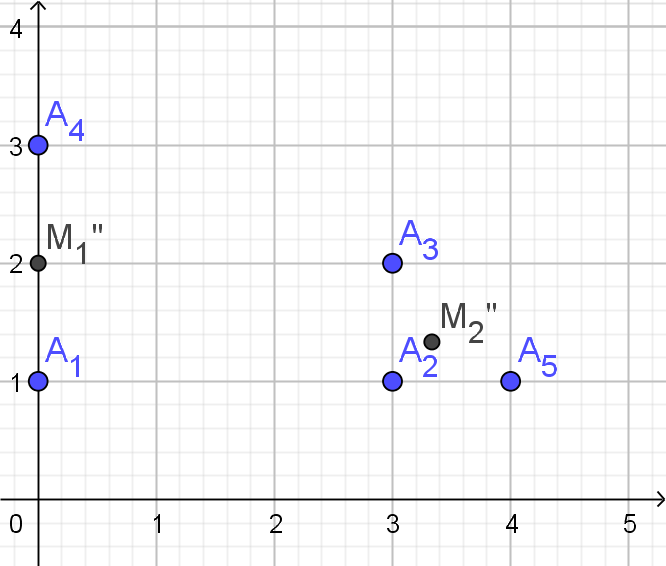
Voorbeeld F

Gegeven een cluster $C$ die de volgende objecten bevat:
xy
$A_{1}$01
$A_{2}$31
$A_{3}$32
$A_{4}$03
$A_{5}$41
We bepalen vooraf dat we twee clusters willen, dus $k=2$.
Geef de uitwerking van de eerste twee iteraties.
Als afstandsmaat gebruik je de normale (Euclidische) afstand.
Start:
Kies twee willekeurig centra. $M_{1}=(2,2)$ en $M_{2}=(3,0)$
Iteratie 1:
  1. De afstandsmatrix wordt:
    $M_{1}$$M_{2}$toewijzing
    $A_{1}$2.243.16$C_{1}$
    $A_{2}$1.411$C_{2}$
    $A_{3}$12$C_{1}$
    $A_{4}$2.244.24$C_{1}$
    $A_{5}$2.241.41$C_{2}$
  2. De nieuwe clusters zijn:
    $C_{1}$$\{A_{1},A_{3},A_{4}\}$
    $C_{2}$$\{A_{2},A_{5}\}$
  3. De nieuwe centra zijn: $M_{1}'=(\frac{0+3+0}{3},\frac{1+2+3}{3})=(1,2)$ en $M_{2}'=(\frac{3+4}{2},\frac{1+1}{2})=(3.5,1)$
Iteratie 2:
  1. De afstandsmatrix wordt:
    $M_{1}'$$M_{2}'$toewijzing
    $A_{1}$1.413.5$C_{1}$
    $A_{2}$2.240.5$C_{2}$
    $A_{3}$21.12$C_{2}$
    $A_{4}$1.414.03$C_{1}$
    $A_{5}$3.160.5$C_{2}$
  2. De nieuwe clusters zijn:
    $C_{1}$$\{A_{1},A_{4}\}$
    $C_{2}$$\{A_{2},A_{3},A_{5}\}$
  3. De nieuwe centra zijn: $M_{1}''=(\frac{0+0}{2},\frac{1+3}{3})=(0,2)$ en $M_{2}''=(\frac{3+3+4}{3},\frac{1+2+1}{3})=(3.33,1.33)$
Een derde iteratie levert hier weer geen verandering. Dus klaar.
Start

Iteratie 1

Iteratie 2

Vragen

  1. Gegeven is een dataset met 6 datapunten.
    $x_{1}$$x_{2}$$x_{3}$$x_{4}$
    $A_{1}$6345
    $A_{2}$2354
    $A_{3}$5463
    $A_{4}$9118
    $A_{5}$8209
    $A_{6}$8018
    Als afstandsmaat gebruiken we de normale (Euclidische) afstand.
    1. Bereken de Euclidische afstand van $A_{1}$ en $A_{2}$ Antwoord $d(A_{1},A_{2})=\sqrt{(6-2)^{2}+(3-3)^{2}+(4-5)^{2}+(5-4)^{2}}=\sqrt{18}=3\sqrt{2}$
    We clusteren deze gegevens in twee clusters: $C_{1}=\{A_{1},A_{2},A_{3}\}$ en $C_{2}=\{A_{4},A_{5},A_{6}\}$
      Vul de volgende afstandsmatrix in: Antwoord
      $A_{4}$$A_{5}$$A_{6}$
      $A_{1}$5.576.085.57
      $A_{2}$9.229.338.77
      $A_{3}$8.669.228.66
    $A_{4}$$A_{5}$$A_{6}$
    $A_{1}$
    $A_{2}$
    $A_{3}$
    1. Geef de afstand tussen de clusters $C_{1}$ en $C_{2}$. Antwoord De afstand tussen $C_{1}$ en $C_{2}$ is de kleinste afstand in de tabel dus: $d(C_{1},C_{2})=5.57$
    2. Bereken de centra van clusters $C_{1}$ en $C_{2}$ Antwoord
      $C_{1}$: centrum $M_{1}=\{4.33,3.33,5,4\}$
      $C_{2}$: centrum $M_{2}=\{8.33,1,0.67,8.33\}$
  2. Gegeven de volgende vier objecten:
    $x_{1}$$x_{2}$
    $O_{1}$22
    $O_{2}$86
    $O_{3}$68
    $O_{4}$24
    Als afstandsmaat gebruiken we de normale (Euclidische) afstand.
    We willen deze gegevens clusteren in twee clusters ($K$=2), met behulp van het $K$-means algoritme.
    Initialiseer het algoritme met: objecten 1 en 3 in één cluster $C_{1}$ en objecten 2 en 4 in de andere cluster $C_{2}$.
    Noteer $C_{1}=\{O_{1},O_{3}\}$ en $C_{2}=\{O_{2},O_{4}\}$
    1. Bereken het centrum $M_{1}$ van $C_{1}$ en het centrum $M_{2}$ van $C_{2}$ Antwoord
      $C_{1}$: centrum $M_{1}=\{4,5\}$
      $C_{2}$: centrum $M_{2}=\{5,5\}$
    2. Vul de volgende afstandsmatrix in en bereken daarmee de afstand tussen clusters $C_{1}$ en $C_{2}$
      $O_{2}$$O_{4}$
      $O_{1}$
      $O_{3}$
      Antwoord
      $O_{2}$$O_{4}$
      $O_{1}$7.212
      $O_{3}$2.835.7
      Dus de afstand $d(C_{1},C_{2})=2$
    3. Bereken de afstanden tot de centra $M_{1}$ en $M_{2}$ en vul de volgende tabel in:
      $M_{1}$$M_{2}$toewijzing
      $O_{1}$
      $O_{2}$
      $O_{3}$
      $O_{4}$
      Antwoord
      $M_{1}$$M_{2}$toewijzing
      $O_{1}$3.64.5$C_{1}$
      $O_{2}$3.63.1$C_{2}$
      $O_{3}$4.13.2$C_{2}$
      $O_{4}$33.2$C_{1}$
    4. Wat zijn uiteindelijk de clusters vanhet $K$-means algoritme. Antwoord
      $C_{1}=\{O_{1},O_{4}\}$ en $C_{2}=\{O_{2},O_{3}\}$ $C_{1}$: centrum $M_{1}'=\{2,3\}$
      $C_{2}$: centrum $M_{2}'=\{7,7\}$
      $M_{1}'$$M_{2}'$toewijzing
      $O_{1}$17.1$C_{1}$
      $O_{2}$6.71.4$C_{2}$
      $O_{3}$6.41.4$C_{2}$
      $O_{4}$15.8$C_{1}$
      Er is geen verandering in de clustering.
      Dus:$C_{1}=\{O_{1},O_{4}\}$ en $C_{2}=\{O_{2},O_{3}\}$
  3. Gegeven de volgende zes datapunten:
    $x_{1}$$x_{2}$
    $D_{1}$63
    $D_{2}$23
    $D_{3}$54
    $D_{4}$91
    $D_{5}$82
    $D_{6}$80
    Als afstandsmaat gebruiken we de normale (Euclidische) afstand.
    We willen deze gegevens clusteren in drie clusters ($K$=3), met behulp van het $K$-means algoritme.
    Initialiseer het algoritme met $C_{1}=\{D_{1},D_{2}\}$ , $C_{2}=\{D_{3},D_{4}\}$ en $C_{3}=\{D_{5},D_{6}\}$
    1. Bereken het centrum $M_{1}$ van $C_{1}$, het centrum $M_{2}$ van $C_{2}$ en het centrum $M_{3}$ van $C_{3}$ Antwoord
      $C_{1}$: centrum $M_{1}=\{4,3\}$
      $C_{2}$: centrum $M_{2}=\{7,2.5\}$
      $C_{3}$: centrum $M_{3}=\{8,1\}$
    2. Bereken de afstanden tot de centra $M_{1}$ en $M_{2}$ en vul de volgende tabel in en voer zonodig een herclustering in:
      $M_{1}$$M_{2}$$M_{3}$toewijzing
      $D_{1}$
      $D_{2}$
      $D_{3}$
      $D_{4}$
      $D_{5}$
      $D_{6}$
      Antwoord
      $M_{1}$$M_{2}$$M_{3}$toewijzing
      $D_{1}$21.12.83$C_{2}$
      $D_{2}$25.06.3$C_{1}$
      $D_{3}$1.42.54.2$C_{1}$
      $D_{4}$5.42.51$C_{3}$
      $D_{5}$4.11.11$C_{3}$
      $D_{6}$52.71$C_{3}$
      Er is de herclustering $C_{1}=\{D_{2},D_{3}\}$ , $C_{2}=\{D_{1}\}$ en $C_{3}=\{D_{4},D_{5},D_{6}\}$
    3. Wat zijn de nieuwe centra en zijn we nu klaar?. Antwoord
      $C_{1}=\{D_{2},D_{3}\}$ , $C_{2}=\{D_{1}\}$ en $C_{3}=\{D_{4},D_{5},D_{6}\}$
      $C_{1}$: centrum $M_{1}'=\{3.5,3.5\}$
      $C_{2}$: centrum $M_{2}'=\{6,3\}$ $C_{3}$: centrum $M_{3}'=\{8.3,1\}$
      $M_{1}'$$M_{2}'$$M_{3}'$toewijzing
      $D_{1}$2.503$C_{2}$
      $D_{2}$1.646.6$C_{1}$
      $D_{3}$1.61.44.5$C_{2}$
      $D_{4}$63.60.7$C_{3}$
      $D_{5}$4.772.271.1$C_{3}$
      $D_{6}$5.73.61.1$C_{3}$
      Er is weer verandering in de clustering.
      Dus:$C_{1}=\{D_{2}\}$ , $C_{2}=\{D_{1},D_{3}\}$ en $C_{3}=\{D_{4},D_{5},D_{6}\}$
      Er is dus minstens nog een iteratie nodig.
  4. Gegeven de volgende vier objecten:
    $x_{1}$$x_{2}$
    $A_{1}$00
    $A_{2}$78
    $A_{3}$48
    $A_{4}$30
    Als afstandsmaat gebruiken we de normale (Euclidische) afstand.
    Cluster de gegevens volledig in twee clusters ($K$=2), met behulp van het $K$-means algoritme.
    Initialiseer het algoritme met de willekeurige centrum $M_{1}=(0,6)$ en $M_{2}=(7,2)$. Vul je resultaten in onderstaande tabel in.
    ClustersCentra
    Start$M_{1}=(0,6)$
    $M_{2}=(7,2)$
    Iteratie 1$C_{1}=$
    $C_{2}=$    		$M_{1}=$
    $M_{2}=$
    Iteratie 2$C_{1}=$
    $C_{2}=$    		$M_{1}=$
    $M_{2}=$
    ...
    Antwoord Iteratie 1:
    $M_{1}$$M_{2}$toewijzing
    $A_{1}$6.007.28$C_{1}$
    $A_{2}$7.286.00$C_{2}$
    $A_{3}$4.476.71$C_{1}$
    $A_{4}$6.714.47$C_{2}$
    ClustersCentra
    Start$M_{1}=(0,6)$
    $M_{2}=(7,2)$
    Iteratie 1$C_{1}=\{A_{1},A_{3}\}$
    $C_{2}=\{A_{2},A_{4}\}$    		$M_{1}=(2,4)$
    $M_{2}=(5,4)$
    Iteratie 2:
    $M_{1}$$M_{2}$toewijzing
    $A_{1}$4.476.40$C_{1}$
    $A_{2}$6.404.47$C_{2}$
    $A_{3}$4.474.12$C_{2}$
    $A_{4}$4.124.47$C_{1}$
    ClustersCentra
    Start$M_{1}=(0,6)$
    $M_{2}=(7,2)$
    Iteratie 1$C_{1}=\{A_{1},A_{3}\}$
    $C_{2}=\{A_{2},A_{4}\}$    		$M_{1}=(2,4)$
    $M_{2}=(5,4)$
    Iteratie 2$C_{1}=\{A_{1},A_{4}\}$
    $C_{2}=\{A_{2},A_{3}\}$    		$M_{1}=(1.5,0)$
    $M_{2}=(5.5,8)$
    Iteratie 3:
    $M_{1}$$M_{2}$toewijzing
    $A_{1}$1.509.71$C_{1}$
    $A_{2}$9.711.50$C_{2}$
    $A_{3}$8.381.50$C_{2}$
    $A_{4}$1.508.38$C_{1}$
    Geen verandering clustering dus klaar.
  5. Een reisagentschap wil zijn klanten opdelen in twee clusters ($K$=2), op basis van leeftijd en duur van geboekte vakanties. De informatie van het reisagentschap is gegeven in de onderstaande tabel. De leeftijd van klanten uitgedrukt in aantal jaren, de duur van de vakantie in het aantal dagen.
    LeeftijdDuur vakantie
    $TO_{1}$193
    $TO_{2}$258
    $TO_{3}$4314
    $TO_{4}$6114
    $TO_{5}$307
    $TO_{6}$2210
    Als afstandsmaat gebruiken we de normale (Euclidische) afstand.
    Cluster de gegevens volledig in twee clusters ($K$=2), met behulp van het $K$-means algoritme.
    Initialiseer het algoritme met de willekeurige centrum $M_{1}=TO_{1}$ en $M_{2}=TO_{2}$. Vul je resultaten in onderstaande tabel in.
    ClustersCentra
    Start$M_{1}=(19,3)$
    $M_{2}=(25,8)$
    Iteratie 1$C_{1}=$
    $C_{2}=$    		$M_{1}=$
    $M_{2}=$
    Iteratie 2$C_{1}=$
    $C_{2}=$    		$M_{1}=$
    $M_{2}=$
    ...
    Antwoord Iteratie 1:
    $TO_{1}$0.007.81 $C_{1}$
    $TO_{2}$7.810.00 $C_{2}$
    $TO_{3}$26.4018.97 $C_{2}$
    $TO_{4}$43.4236.50 $C_{2}$
    $TO_{5}$11.705.10 $C_{2}$
    $TO_{6}$7.623.61 $C_{2}$
    ClustersCentra
    Start$M_{1}=(19,3)$
    $M_{2}=(25,8)$
    Iteratie 1$C_{1}=\{TO_{1}\}$
    $C_{2}=\{TO_{2},TO_{3},TO_{4},TO_{5},TO_{6}\}$    		$M_{1}=(19,3)$
    $M_{2}=(36.2,10.6)$
    Iteratie 2:
    $M_{1}$$M_{2}$toewijzing
    $TO_{1}$0.0018.80 $C_{1}$
    $TO_{2}$7.8111.50 $C_{1}$
    $TO_{3}$26.407.60 $C_{2}$
    $TO_{4}$43.4225.03 $C_{2}$
    $TO_{5}$11.707.17 $C_{2}$
    $TO_{6}$7.6214.21 $C_{1}$
    ClustersCentra
    Start$M_{1}=(0,6)$
    $M_{2}=(7,2)$
    Iteratie 1$C_{1}=\{TO_{1}\}$
    $C_{2}=\{TO_{2},TO_{3},TO_{4},TO_{5},TO_{6}\}$    		$M_{1}=(19,3)$
    $M_{2}=(36.2,10.6)$
    Iteratie 2$C_{1}=\{TO_{1},TO_{2},TO_{6}\}$
    $C_{2}=\{TO_{3},TO_{4},TO_{5}\}$    		$M_{1}=(1.5,0)$
    $M_{2}=(5.5,8)$
    Iteratie 3:
    $M_{1}$$M_{2}$toewijzing
    $TO_{1}$5.0027.09 $C_{1}$
    $TO_{2}$3.1620.01 $C_{1}$
    $TO_{3}$22.142.87 $C_{2}$
    $TO_{4}$39.6216.50 $C_{2}$
    $TO_{5}$8.0015.39 $C_{1}$
    $TO_{6}$3.0022.73 $C_{1}$
    ClustersCentra
    Start$M_{1}=(0,6)$
    $M_{2}=(7,2)$
    Iteratie 1$C_{1}=\{TO_{1}\}$
    $C_{2}=\{TO_{2},TO_{3},TO_{4},TO_{5},TO_{6}\}$    		$M_{1}=(19,3)$
    $M_{2}=(36.2,10.6)$
    Iteratie 2$C_{1}=\{TO_{1},TO_{2},TO_{6}\}$
    $C_{2}=\{TO_{3},TO_{4},TO_{5}\}$    		$M_{1}=(22,7)$
    $M_{2}=(44.7,11.7)$
    Iteratie 3$C_{1}=\{TO_{1},TO_{2},TO_{5},TO_{6}\}$
    $C_{2}=\{TO_{3},TO_{4}\}$    		$M_{1}=(24,7)$
    $M_{2}=(52,14)$
    Iteratie 4:
    $M_{1}$$M_{2}$toewijzing
    $TO_{1}$6.4034.79 $C_{1}$
    $TO_{2}$1.4127.66 $C_{1}$
    $TO_{3}$20.259.00 $C_{2}$
    $TO_{4}$37.669.00 $C_{2}$
    $TO_{5}$6.0023.09 $C_{1}$
    $TO_{6}$3.6130.27 $C_{1}$
    Geen verandering in clusters dus klaar.
  6. Hieronder staan gegevens van 4 (fictieve) studenten van een data mining cursus. We noteren respectievelijk het aantal bijgewoonde lessen, het aantal dagen examenvoorbereiding, en of ze al dan niet voor het examen kwamen opdagen: $D=\{S_{1}(0.0,0,1),S_{2}(7.8 ,2,1),S_{3}(4.8,2,1),S_{4}(3.0,0,1)\}
    We willen deze objecten clusteren, wat we kunnen doen door middel van de $K$-means methode. Kies $K=2$, en als initiële willekeurige cluster centra: $M_{1}=(0.6,1,0)$ en $M_{2}=(7.2,1,0)$. Pas de $K$-means methode toe op $D$ tot een maximum van 3 stappen. Noteer voor elke iteratie welke clusters gevormd worden en wat de centra zijn.
    Convergeert de methode? Zo ja, leg uit.
    Vul de resultaten in de onderstaande tabel in:
    ClustersCentra
    Start$M_{1}=(0.6,1,0)$
    $M_{2}=(7.2,1,0)$
    Iteratie 1$C_{1}=$
    $C_{2}=$    		$M_{1}=$
    $M_{2}=$
    Iteratie 2$C_{1}=$
    $C_{2}=$    		$M_{1}=$
    $M_{2}=$
    ...
    Antwoord Iteratie 1 :
    $M_{1}$$M_{2}$toewijzing
    $S_{1}$1.547.34$C_{1}$
    $S_{2}$7.341.54$C_{2}$
    $S_{3}$4.432.79$C_{2}$
    $S_{4}$2.794.43$C_{1}$
    ClustersCentra
    Start$M_{1}=(0.6,1,0)$
    $M_{2}=(7.2,1,0)$
    Iteratie 1$C_{1}=\{S_{1},S{4}\}$
    $C_{2}=\{S_{2},S{3}\}$    		$M_{1}=(1.5,0,1)$
    $M_{2}=((6.3,2,1)$
    Iteratie 2:
    $M_{1}$$M_{2}$toewijzing
    $S_{1}$1.506.61$C_{1}$
    $S_{2}$6.611.50$C_{2}$
    $S_{3}$3.861.50$C_{2}$
    $S_{4}$1.503.86$C_{1}$
    Geen verandering in clusters dus klaar.